ریاضیات مهندسی (میکروطبقه بندی شده)
کلیه رشته های فنی و مهندسی کتاب ریاضی مهندسی با نگارش ساده و اجتناب از بيان مطالب غير ضروري سعی داشته كه دانشجويان آزمون كارشناسي ارشد دركمترين زمان بهترين نتيجهگيري را داشته ونياز به كتب ديگر نداشته باشند.
مشاهده توضیحات کامل شابک: 9789641139515
تعداد صفحات: 516
نوبت چاپ: 24
تاریخ چاپ: 1398
مولف : مهندس حسین نامی
برای دانلود رایگان کتاب ریاضیات مهندسی (میکروطبقه بندی شده) مدرسان شریف (بخشی از کتاب) برروی لینک زیر کلیک نمایید. دانلود قسمتی از کتاب نوع فایل: pdf
حجم فایل: 1MB

افزايش روزافزون فارغ التحصيلان دورههاي كارشناسي و کارشناسی ارشد و اشتياق آنها براي ورود به دورههاي كارشناسي ارشد و دکتری و كمبود كتب مناسب جهت آمادگي آزمونهاي كارشناسي ارشد و دکتری، هدف اصلي نگارش و چاپ اين كتاب ميباشد.
با توجه به اين كه درس «رياضيات مهندسي» معمولاً در سال دوم تحصيلي توسط دانشجويان دورههاي كارشناسي گذرانده ميشود و پس از گذشت دو سال از آن، مطالب فرا گرفته شده تقريباً به فراموشي سپرده ميشود، لذا اين كتاب با نگارش ساده و اجتناب از بيان مطالب غيرضروري (اثبات فرمولها و …) سعي بر اين داشته كه دانشجويان جهت موفقيت در آزمون كارشناسي ارشد در كمترين زمان بهترين نتيجهگيري را داشته و ديگر نيازي به مراجعه به كتب ديگر نداشته باشند. از ويژگيهاي بارز اين كتاب نسبت به ديگر كتب موجود در اين زمينه موارد زير را ميتوان نام برد:
۱) مطالب کتاب به صورت کاملاً ساده و با توضیحات فارسی فراوان به همراه مثالهای تألیفی فراوان ارائه شده است و عقیده دارم با خواندن این کتاب نیاز به خواندن هیچ کتاب دیگری در این درس نخواهید داشت.
۲) هر فصل کتاب به صورت میکروطبقهبندی جمعآوری شده است. به این مفهوم که هر فصل به زیربخشهایی تحت عنوان «درسنامه» تقسیم شده وسؤالات و پاسخهای تشریحی آزمونهای گذشته (۸۰ تا ۹۷) به همراه مثالهای تألیفی که مربوط به آن درسنامه هستند، زیر مبحث مربوط به خود آورده شده است تا خواننده پس از فراگیری مطالب مربوطه، تستهای آزمونها را نیز مرور کند. این روش، ذهن را بسیار منظم کرده و انگیزه و اشتیاق یادگیری را بالاتر میبرد.
۳) كتاب حدوداً شامل ۱۰۰۰تست با پاسخهاي كاملاً تشريحي غیرتکراری است كه از اين حيث هم ميتوان كتاب را در بين كتب رياضي مهندسي ديگر كه براي اين منظور تهيه شدهاند، بينظير دانست.
۴) در هر فصل (خصوصاً دو فصل آخر) روشهای تستی و رد گزینه گنجانده شده که این قسمت روشهای حل سریع و بسیار کوتاه سؤالات آن فصل را بررسی کرده است، كه البته حل تشریحی این نوع سؤالات نیز بعضاً در متن کتاب ارائه شده است.
۵) سؤالات دکتری سالهای ۹۱ تا ۹۷ هم در متن درس در درسنامه مربوطه گنجانده شده است.
۶) در انتهاي كتاب سؤالات آزمون كارشناسي ارشدو دکتری سال ۱۳۹۸ به همراه پاسخهاي كاملاً تشريحي ارائه شده است.
۷) مطالب كتاب به گونهاي تدوين گرديده كه ميتواند به عنوان مرجع كامل درس رياضيات مهندسي جهت موفقيت در امتحانات پايان ترم دانشگاهها مورد استفاده قرار گيرد.
۸) فصول اين کتاب برخلاف بعضی کتب (حتی مراجع معتبر!) که به نظر بنده ترتیب مناسبي ندارند، تنظیم شده است؛
به این شکل که ابتدا در چهار فصل نخست، بحث توابع مختلط به طور کامل پشت سرهم بیان شده و در دو فصل آخر، «آنالیز فوریه» و «معادلات دیفرانسیل با مشتقات جزئی» که ارتباط تنگاتنگی با هم دارند، آورده شده است.
با توجه به اينكه هيچ تأليفي خالي از اشكال نيست، لذا از همه استادان و دانشجويان تقاضا دارم، اشكالات اين كتاب را از طريق وب سایت شخصی اینجانب به آدرس www.h-nami.irاطلاع دهند. در ضمن در این وب سایت پشتیبانی و رفع اشکال درسی نیز صورت میگیرد.
در خاتمه جا دارد از خانم فاطمه هليلي كه تايپ و صفحهآرايي اين مجموعه را به عهده داشتند، نهايت سپاسگزاري را داشته باشم.
فصل اول: اعداد و توابع مختلط
درسنامه (1): اعداد مختلط و خواص آن ....................... 1
اعداد مختلط.............................................. 1
اعمال حسابي در اعداد مختلط.............................. 2
مزدوج يك عدد مختلط...................................... 2
خواص اعداد مختلط........................................ 2
ضرب داخلي و خارجي دو عدد مختلط.......................... 2
شكل قطبي اعداد مختلط.................................... 3
محاسبهي اندازه و آرگومانِ اعداد مختلط................... 3
تبديل فرم دكارتي به فرم قطبي............................ 4
شكل نمايي عدد مختلط..................................... 4
ضرب و تقسيم اعداد مختلط به فرم قطبي يا نمايي........... 5
توان يك عدد مختلط و فرمول دموآور........................ 5
ريشهي يك عدد مختلط...................................... 6
چند نکته در مورد ریشههای nام عدد یک..................... 7
معادلات مختلط............................................. 7
چند قضيهي مهم............................................ 8
نواحي در صفحه مختلط..................................... 9
بررسي معادلهي چند شكل خاص.............................. 11
درسنامه (2): توابع مختلط ................................ 13
نقاط شاخهای و خطوط شاخهای.............................. 13
تابع نمايي............................................ 14
توابع مثلثاتي مختلط.................................... 14
لگاريتم يك عدد......................................... 17
مقدار اصلي لگاريتم، نقطهي شاخهاي و خطوط شاخهاي........ 17
توابع تواني به صورت ................................. 19
توابع هذلولي مختلط..................................... 20
توابع مثلثاتي و هيپربوليك معكوس........................ 22
روابط مهم توابع معكوسِ هيپربوليك........................ 22
درسنامه (3): حد و پيوستگي، مشتقپذيري، روابط كوشي ريمان و توابع تحليلي .................................................. 23
حد و پیوستگی توابع مختلط............................... 23
روشهای بهدست آوردن حد و اثبات عدم وجود حد توابع مختلط. 23
مشتق توابع مختلط....................................... 24
قضاياي كوشي ريمان...................................... 25
توابع تحليلي............................................ 26
صورتهاي ديگر كنترل برقراري شرايط كوشي ريمان........... 26
بررسی تحلیلی بودن توابع چندضابطهای.................... 27
عکس قضیه کوشی ریمان.................................... 28
معادلات کوشی ریمان در مختصات قطبی...................... 30
الگوريتم ارتباط بين روابط كوشي ريمان، مشتقپذيري و تحليلی بودن........................................................ 34
اصل بازتاب.............................................. 35
درسنامه (4): توابع همساز و بدست آوردن مزدوج همساز ......... 38
توابع همساز............................................... 38
مزدوج همساز و روشهای بهدست آوردن آن...................... 41
روش اولِ بهدست آوردن مزدوج همساز............................ .... 41
روش دومِ محاسبهی مزدوج همساز............................. 42
روش بهدست آوردن ضابطه تابع تحليلي..................... 44
روش سريع در بهدست آوردن f(z) از روي u و v در برخي سؤالات خاص 46
فصل دوم: نگاشت
درسنامه (1): تعریف نگاشت و نگاشت همدیس .................... 47
تعريف نگاشت............................................... 47
نگاشت همديس (حافظ زاويه)................................. 47
درسنامه (2): انواع نگاشت................................... 49
نگاشت هماني....................................... 49
نگاشت انتقال....................................... 49
نگاشت ............................................... 49
نگاشت خطي.......................................... 49
نگاشت................................................ 49
نگاشت................................................. 50
نگاشت ................................................. 50
نگاشت ................................................ 50
نگاشت................................................. 53
نگاشت................................................ 54
نگاشت............................................... 54
نگاشتهاي............................................ 58
نگاشتهاي و.................................. 58
نگاشت............................................... 59
نگاشت خطي كسري (نگاشت دو خطي يا موبيوس)........... 61
درسنامه (3): تبديل سه نقطه توسط نگاشت كسري و تعریف نقاط ثابت یک نگاشت 63
تبدیل سه نقطه توسط نگاشت کسری ........................... 63
نقاط ثابت يك نگاشت........................................ 64
درسنامه (4): نگاشتهای ترکیبی و متوالی...................... 65
جمعبندی انواع سؤالاتی که در حوزه نگاشت مطرح میشود........ 71
درسنامه (5): محاسبه مساحت تبدیلیافته یک ناحیه.............. 76
فصل سوم: انتگرالگيري از توابع مختلط
مقدمه................................................... 78
نواحی همبند ساده و همبند چندگانه....................... 79
درسنامه (1): انتگرال توابع غيرتحليلي..................... 80
شكل مختلط قضيه گرين.................................... 84
درسنامه (2): انتگرالگیری از توابعي كه تحليلي هستند يا فقط در چند نقطه غير تحليلي هستند.................................... 87
قضيه كوشي ـ گورسا...................................... 87
فرمول انتگرال كوشي..................................... 87
قضيه (تعميم قضيه كوشي براي نواحي همبند چندگانه)....... 88
استفاده از فرمول تابع اوليه و انتگرالگيري عادي........ 90
درسنامه3: چند قضیه مهم در مورد توابع مختلط............... 91
كران بالاي قدر مطلق يك انتگرال مختلط................... 91
نامساوي كوشي............................................ 91
قضيه موررا.............................................. 91
قضيه مدول ماكزيمم (اصل ماكزيمم قدر مطلق) و مدول مينيمم (اصل مينيمم قدر مطلق)............................................... 92
قضيه ليوويل............................................. 94
قضيه اصلي جبر........................................... 95
قضيه مقدار ميانگين گاوس................................ 96
فصل چهارم: سريهاي مختلط، محاسبه مانده و انتگرالگيري به كمك قضيه ماندهها
درسنامه (1): سريهاي مختلط ............................... 97
دنبالههاي مختلط........................................ 97
سريهاي مختلط............................................ 98
تعريف همگرايي مطلق و مشروط............................. 98
سريهاي تواني و بهدست آوردن شعاع همگرايي آنها.......... 98
سريهاي تابعي و بهدست آوردن ناحيه همگرايي آنها......... 99
قضيه تيلور............................................. 101
دستهبندی روشهای به دست آوردن بسطهای مکلورن........... 101
قضيه لوران (لورانت)................................... 105
دستورالعمل نوشتن بسط لوران برای توابع کسری........... 106
خلاصه و جمعبندی روش نوشتن بسط لوران در توابع کسری..... 108
درسنامه (2): انواع نقاط تكين و محاسبه مانده ............ 115
تعريف نقطه تكين....................................... 115
تكين برداشتني......................................... 117
تكين اساسي........................................... 117
قطب.................................................... 118
تعيين مرتبه قطب....................................... 118
دستهبندی نقاط تکین.................................... 119
صفر تابع................................................ 120
مانده (باقیمانده) f(z) در یک نقطه....................... 121
روش اول در محاسبهی مانده............................... 121
روش دوم در محاسبه مانده................................ 125
روش سوم در محاسبه مانده................................ 126
محاسبه مانده توابع خاص................................. 126
بررسي رفتار تابع در بينهايت............................ 130
محاسبه مانده در بينهايت................................ 130
درسنامه (3): محاسبهي انتگرال توابع مختلط به كمك قضيه ماندهها ........................................................ 132
محاسبهی راحتتر انتگرال با استفاده از قطبهای خارج از مرز 152
نكتهي تكميلي قضيه ماندهها.............................. 153
درسنامه (4): محاسبهي انتگرال توابع حقيقي و برخي سريهاي عددي به كمك قضيه ماندهها ........................................... 156
1ـ محاسبه انتگرالهايي به صورت............. 156
2ـ محاسبه انتگرالهايي به فرم كلي............ 157
3ـ محاسبه انتگرالهايي به فرم كلي و 159
4ـ محاسبه نوع ديگري از انتگرالهاي حقيقي............... 162
محاسبهي انتگرالهايي كه تابع زير انتگرال داراي نقطه يا خط شاخهاي است 166
جواب نهايي چند انتگرال مهم............................. 173
بهدست آوردن مقدار بعضي از سريها با كمك گرفتن از روش ماندهها 173
نظريه ماندهها و محاسبهي معكوس لاپلاس تابع............... 174
درسنامه (5): چند قضیه مفهومی ریاضی...................... 176
قضيه شناسه.............................................. 176
اصل آوند................................................ 176
قضيه روشه............................................... 177
فصل پنجم: سري فوريه، انتگرال و تبديل فوريه
درسنامه (1): سری فوریه.................................. 179
مقدمه................................................... 179
روش انتگرالگيري جزء به جزء............................. 180
انتگرالگيري جزء به جزء به كمك تشكيل جدول.............. 181
توابع به طور مجازي متناوب.............................. 184
ضرب داخلی توابع ـ تعامد................................ 186
سري فوريه............................................... 187
خلاصه روش حل و نكات مهم در مسائل سري فوريه............. 187
بسطهاي نيمدامنهاي (سريهاي فوريه سينوسي و كسينوسي)..... 196
ایستگاه نکات مهم تستی شماره (1): بدست آوردن مقدار سري فوريه در يك نقطهی خاص 203
ایستگاه نکات مهم تستی شماره (2): مطالب مهم در حل برخي تستهاي سري فوريه 208
ایستگاه نکات مهم تستی شماره (3): داستان علامت اولين كسينوس و سينوس.................................................. 211
داستان تقارن نيمموج (داشتن هارمونيكهاي زوج يا فرد)... 214
شرایط وجود سری فوریه.................................. 218
قضيه ديريكله.......................................... 219
سرعت همگرايي ضرايب سري فوريه.......................... 221
وجود تقارن مخفي....................................... 224
مشتقگيري از سري فوريه................................. 225
انتگرال گیری از سری فوریه............................. 225
سري فوريه مختلط....................................... 229
سري فوريه دوگانه...................................... 230
انواع ديگر سريهاي فوريه............................... 232
سري لژاندر ـ فوريه.................................... 232
سريهاي بسل ـ فوريه.................................... 233
تقریب به وسیلهی توابع مثلثاتی (کمترین مجموع مربعات خطا) 234
درسنامه (2): تساوي پارسوال و محاسبهي سريهاي عددي........ 236
تساوي پارسوال......................................... 236
روش محاسبهی بعضي از سريهاي عددي....................... 236
ایستگاه نکات مهم تستی شماره (4): بدست آوردن حاصل سريهاي عددي به روش سریع............................................... 242
ضرب داخلي سريهاي فوريه................................ 249
درسنامه (3): انتگرال فوریه ............................ 250
انتگرال فوريه......................................... 250
چند نکته که در حل سریع سؤالات انتگرال فوریه به ما کمک میکند 251
شرايط ديريكله......................................... 252
انتگرال فوريه سينوسي و كسينوسي........................ 254
انتگرال فوريه مختلط................................... 263
رابطه پارسوال در انتگرال فوريه........................ 263
درسنامه (4): تبدیل فوریه................................ 266
تبديل فوريه نامتناهي.................................. 266
تبديل فوريه كسينوسي و سينوسي نامتناهي................ 272
تبديل فوريه كسينوسي و سينوسي متناهي.................. 272
برخي از خواص تبديل فوريه.............................. 274
استفاده از تبديل لاپلاس در حل مسائل انتگرال و تبديل فوريه 285
تبديل فوريه تعميم يافته............................... 287
فصل ششم: معادلات ديفرانسيل با مشتقهاي جزئي
درسنامه (1): مسائل اشتروم ـ ليوويل و روش تفكيك متغيرها در حل معادلات ديفرانسيل با مشتقات جزئي ................................ 290
مفاهيم اوليه معادلات ديفرانسيل با مشتقات جزئي......... 290
انواع شرايط مرزي...................................... 292
مسائل اشتروم ـ ليوويل عادی............................ 292
مسأله اشتروم ـ ليوويل متناوب.......................... 296
مسأله اشتروم ـ ليوويل منفرد........................... 298
حل معادلات با مشتقهاي جزئي به روش جداسازی متغيرها (روش ضربی)....................................................... 298
چه نوع معادلاتی را میتوان با استفاده از روش جداسازی متغیرها حل نمود؟.................................................. 303
روش سه گام در حل معادلات ديفرانسيل با مشتقات جزئي مرتبه دوم با استفاده از تفكيك متغيرها.............................. 305
درسنامه (2): حل و بررسي معادله موج ..................... 316
معادلهی موج متناهی.................................... 316
فرم استاندارد و همگن معادلهی موج..................... 316
فرم کلی جواب و مقادیر ویژه معادلهی موج همگن.......... 318
معادلهی موج در فواصل نیمهمتناهی و نامتناهی........... 320
معادلهی موج نامتناهی.................................. 320
روش تستی قسمت اول: صدق کردن شرایط مرزی در معادله..... 322
روش تستی قسمت دوم: چند نکته دیگر در مورد معادلهی موج همگن 326
امواج ميرا............................................ 328
جواب دالامبر معادله موج................................ 330
دستورالعمل حل دالامبر معادله موج به روش جبري.......... 331
ملاحظاتي مفهومي دربارهي حل دالامبر معادله موج متناهي.. 344
حل دالامبر معادلهي موج براي دو حالت نامتناهي و نيمه متناهي 346
چند مثال متنوع ديگر از حل دالامبر معادله موج.......... 349
امواج ساكن و امواج متحرك.............................. 353
درسنامه (3): حل و بررسی معادله گرما .................... 355
معادلهي انتقال حرارت در يك ميلهي متناهي.............. 355
فرم كلي جواب ـ يافتن مقادير و توابع ويژه در معادله گرمای استاندارد............................................. 358
نکات تستی برای حل سؤالات معادلهی گرما................. 362
مسأله گرما براي يك ميله نامتناهي..................... 372
مسأله گرما براي يك ميله نيمهمتناهي................... 375
درسنامه (4): حل و بررسي معادلهي لاپلاس ................... 378
بحث در مورد....................................... 381
روشهای تستی برای حل سؤالات معادلات لاپلاس................ 389
تعريف معادله پواسون................................... 396
معادله لاپلاس در مختصات قطبي............................ 396
مقدار جواب در مرکز دایره.............................. 407
معادله لاپلاس در مختصات كروي............................ 414
مسأله ديريكله براي نيمصفحه (فرمول پوآسون براي نيمصفحه) 418
مسأله ديريكله براي دايره يكه (فرمول پوآسون).......... 419
كاربرد نگاشت همديس در حل مسأله لاپلاس.................. 419
بررسي معادلات موج و گرماي دو بعدي........................ 423
معادله موج دو بعدي در دستگاه مختصات قطبي............. 426
خلاصهي حل معادلهي لاپلاس همگن در دستگاه دكارتي.......... 429
خلاصهي حل معادلهي گرما (انتقال حرارت) در دستگاه دكارتي 429
خلاصهي حل معادلهي موج در دستگاه دكارتي................ 429
جمعبندي نوع جوابها.................................... 429
درسنامه (5): حل و بررسي معادلات ناهمگن................... 430
روش حل معادلات همگن با شرايط مرزي غيرهمگن............. 430
تغيير متغير در معادلاتي كه شرايط مرزي آنها ناهمگن باشد 430
روش حل معادلات ناهمگن كه شرايط مرزي همگن دارند........ 433
الف) حل معادلاتی که عامل ناهمگن معادله به زمان وابسته نیست 433
ب) حل معادلاتی که عامل ناهمگن معادله به زمان هم وابسته است. (حل براساس توابع ويژه).................................... 436
روش حل معادلات مرتبهي دوم ناهمگن با شرايط مرزي ناهمگن 441
تغییر متغیر در حل معادله ی لاپلاس قطبی غیرهمگن......... 447
حل معادلهي موج ناهمگن به روش دالامبر.................. 452
جمعبندي روشهاي حل معادله موج به روش دالامبر........... 457
درسنامه (6): استفاده از تبدیلات انتگرالی در حل معادلات دیفرانسیل با مشتقات جزئی............................................. 458
حل معادلات با مشتق جزئي با استفاده از تبديل لاپلاس...... 458
استفاده از تبديل فوريه در حل معادلات با مشتقهاي جزئي.. 470
تبديل فوريه سينوسي و كسينوسي نامتناهي................ 472
تبديل فوريه سينوسي و كسينوسي متناهي.................. 473
درسنامه (7): دستهبندي معادلات با مشتقات جزئي، روشهاي حل و فرم استاندارد اين نوع معادلات .......................................... 475
بهدست آوردن تغيير متغيرهاي لازم براي رسيدن به فرم كانونيك 476
روشهاي تشكيل معادلات ديفرانسيل با مشتقهاي جزئي........ 482
روشهاي حل معادلات ديفرانسيل با مشتقهاي جزئي........... 485
1) استفاده از روشهاي حل معادلات ديفرانسيل معمولي و انتگرالگيري....................................................... 485
2) حل معادلاتي به فرم كلي................... 488
3) حل معادلاتي به فرم كلي............... 488
4) روشهای پراکنده دیگری همچون آنچه در مورد روش ضربی گفتیم و یا استفاده از تغییر متغیرهای گوناگون و نظایر آن هم برای حل برخی معادلات کاربرد دارد ................................... 491
حل معادلات ديفرانسيل با مشتقات جزئي مرتبه دوم با ضرايب ثابت 493
5) حل معادلات خطي مرتبه اول با استفاده از دستگاه لاگرانژ 494
ایستگاه نکات مهم تستی شماره (5): چند نكته در مورد انواع معادله ديفرانسيل با مشتقات جزئي ............................. 498
..........................................................
سؤالات آزمون مهندسی برق ـ الکترونیک ـ دکتری 98 ....... 501
پاسخنامه آزمون مهندسی برق ـ الکترونیک ـ دکتری 98 .... 503
سؤالات آزمون مهندسی برق و مکانیک ـ سراسری 98 ......... 509
پاسخنامه آزمون مهندسی برق و مکانیک ـ سراسری 98 ...... 510
منابع و مراجع ........................................ 516
- دانلود فایل قسمتی از کتاب ریاضیات مهندسی میکرو چاپ بیست و چهارم
- دانلود فایل پاسخنامه آزمونهای خودسنجی- چاپ اول تا دهم
- دانلود فایل پاسخنامه تست های تکمیلی- چاپ بیست و یکم
- دانلود فایل پاسخنامه آزمونهای خودسنجی- چاپ یازدهم تا شانزدهم
- دانلود فایل پاسخنامه آزمونهای خودسنجی- چاپ هفدهم تا نوزدهم
- دانلود فایل پاسخنامه تست های تکمیلی- چاپ بیستم
- دانلود فایل پاسخنامه تست های تکمیلی- چاپ بیست و دوم
- دانلود فایل پاسخنامه تست های تکمیلی- چاپ بیست و سوم
-
دانلود فایل قسمتی از کتاب ریاضیات مهندسی چاپ بیست و سوم
- فصل اول: اعداد و توابع مختلط
- فصل دوم: نگاشت
- فصل سوم: انتگرال گيري از توابع مختلط
- فصل چهارم: سريهاي مختلط، محاسبه مانده و انتگرال گيري به كمك قضيه ماندهها-قسمت اول
- فصل چهارم: سريهاي مختلط، محاسبه مانده و انتگرال گيري به كمك قضيه ماندهها-قسمت دوم
- فصل چهارم: سريهاي مختلط، محاسبه مانده و انتگرال گيري به كمك قضيه ماندهها-قسمت سوم
- فصل پنجم: سري فوريه، انتگرال و تبديل فوريه
- فصل ششم: معادلات ديفرانسيل با مشتقهاي جزئي-قسمت اول
- فصل ششم: معادلات ديفرانسيل با مشتقهاي جزئي-قسمت دوم
- فصل ششم: معادلات ديفرانسيل با مشتقهاي جزئي-قسمت سوم
- دانلود فایل مثالهای اضافی برای تمرین بیشتر - ریاضیات مهندسی-چاپ بیست و چهارم
- ساکتیان
تشکر
- محمد
- محمد


- حسن
استاد برای حل معادلات موج ناهمگن به جای استفاده از روش دالامبر تعمیم یافته(برای اینکه فرمول جدید حفظ نکنیم) میشه از روش عادی تغییر متغییر استفاده کرد؟ سوال 1 صفحه 654 چاپ 22 را هر چقدر حل میکنم با روش عادی به جواب نمیرسم،لطفا راهنمایی کنید.
- nima hadi
- nima hadi
ببخشید تو چاپ بیستم صفحه 589 مثال 18 فرمول میانگین پتانسیل گفته شده چجوری بدست اومد ، من تو فصل انتگرالهای مختلط چنین فرمولی ندیدم
- حسن
استاد سوال 9 صفحه 567 مگر نسبت به t مشتق نگرفتیم از طرفین تساوی پس چرا در پاسخنامه ، از تابع G نسبت به x مشتق گرفته شده؟
- Salar.F.R
مباحث درس ریاضی مهندسی رشته مکانیک با بقیه رشته های فنی مهندسی فرق دارند؟
واسه کنکور کارشناسی ارشد باید برای رشته مکانیک چه مباحثی رو بخونم که سر جلسه امتحان وقتم هدر نرود؟
اما اینکه بتوان فصلی را سلکت کرد ،امکان ندارد،چون سال به سال فرق می کند.موفق باشید
- nima hadi
درضمن مشکل ورود به پنل کاربری حل شده نیاز به بررسی نیست.
باتشکر
- سعید
ببخشید مهندس ، صفحه 568 کتاب ریاضی مهندسی چاپ 22 سوال 19 ، g فقط نسبت به x و L فرده ، چطور در نقطه دوم سوال : g(-x+at( برابر شده با
(g(x-at-
با تشکر
- nima hadi
حال اگر -n قرار بدیم که به خودش نمیرسیم!
- حسن
استاد دو سوال در مورد درس ریاضی مهندسی:
1. در مورد اصل بازتاب مگر نباید تابع روی قسمت محور حقیقی که متقارن است تحلیلی باشد، سوال 13 صفحه 63 چاپ 22 چطوری حل شده؟
2. در مورد سوال 76 صفحه 133 چاپ 22 ، واقعا متوجه نشدم چطوری راه حل دوم را عدد گذاری کنم که به جواب برسم؟ لطفا یه کم بیشتر در مورد نگاشت معکوس نگاشت موبیوس توضح می دهید؟
2-در مورد نگاشت معکوس موبیوس کافی است z را برحسب w محاسبه کنیم و اگر مثلا نگاشت z=f(w) ناحیه Im(w) بزرگتر از صفر را به درون دایره واحد نگاشت می کرد ،نگاشت w=f^-1(z) درون دایره واحد را به ناحیه Im(w) بزرگتر از صفر نگاشت می کند.
- سینا
- محمد امین میرزایی
بسیار ممنونم بابت کتاب خوب و کاملتون
- Shakiba
من به تازگی قسمت سری فوریه در ریاضی مهندسی بدون دخالت دست بعد از درسنامه ان را تمام کرده ام. برای حل یک تیپ سوال با عنوان "سری فوریه تابع f کدام است؟" موارد زیادی باید چک شود.با توجه به اینکه حل یک تیپ سوال مدنظر ماست ایا بهتر نیست زمانی ک برای بررسی موارد زیادی ک مطرح کردید, را روی حل سوال با استفاده از فرمول اصلی سری فوریه بگذاریم؟؟؟؟؟ مطمئنا اگر امکان خطا در حل فرمول اصلی باشد, همان مقدار احتمال خطا در غلط چک کردن موارد بدون دخالت دست هم وجود خواهد داشت...
این موضوع کاملاً سلیقه ایست.شما فقط به یک عنوان سوال اشاره کرده اید که شاید این موضوع صحیح باشد اما توجه کنید که داوطلبان ضعیف هم این کتاب را مطالعه می کنندو در واقع آن ها حتی انتگرال گیری ساده را هم بلد نیستند،ضمناً برخی داوطلبان قوی با توجه به تابع f هم می توانندسریع به جواب برسند.
- zahra
هنوز این قسمت آماده نشده است.
- سعید
توی مثال 4 صفحه 50 چاپ 22 چطور z+1 برابر با re3p/4i میشه؟
با تشکر
- سعید
در مورد مثال 18 صفحه 38 کتاب ریاضی مهندسی چاپ 22 ، توی روش اول 2np از کجا اومده؟
خواص Ln رو می دونم که 2np به تتا اضافه میشه ، ولی این یکی رو نمی دونم دقیقاً از کجا اومده
باتشکر
- سامان
- افشین رحمانی نژاد
لطفا در مورد رابطه هارمونیکهای زوج و فرد با توابع زوج و فرد توضیح بدهید.
مثالهای 20و21 ص 376و377 ریاضی مهندسی (چاپ بیستم)را خواندم و یک
نکته اصلی را نفهمیدم.لطفا توضیح دهید:
چرا در تابع زوج مثال 20 که فقط هارمونیکهای فرد دارد نسبت به x=1بایدتقارن فرد داشته باشد ولی در تابع فرد مثال21که بازهارمونیکهای فرد دارد نسبت به x=pi بایدتقارن زوج داشته باشد.لطفا توضیح دهید.
- امیرحسین
در سوال ۳۹ که انتگرال گرفتید چرا بازه انتگرال رو صفر تا یک در نظر گرفتید
متشکر
t+it→z=0,t=0 و هم چنین z=1+i,t=1
در نتیجه در انتگرال گیری در بازه t انتگرال می گیریم یعنی صفر تا 1.
موفق باشید
- محمدمهدی ظفرمند
با سپاس فراوان
- زهرا درستی
با عرض سلام و خسته نباشید
در سوال 45 آزمون آزمایشی شماره 10 مدرسان شریف رشته هوافضا، اگر در سری فوریه ی داده شده به جای x اعدادصفر و پی را قرار دهیم حاصل سری صفر خواهد شد ، این اتفاق تنها در گزینه ی 2 سوال می افتد اما جواب درست گزینه ی 4 است، اگر امکانش هست در مورد این تناقض برای بنده توضیحاتی بفرمایید.
کتاب حل سوالات ریاضیات مهندسی بدون دخالت دست شما فوق العاده است.
همیشه پیروز و سربلند باشید
- امیرحسین
لطفا فرمول کامل ضرب داخلی سری فوریه را که در کنکور ۹۵ آمده را بنویسید
با تشکر
- آرش
من 5 6 تا سوال ازتون پرسیدم متاسفانه هیچکدومو پاسخ ندادید مشکل از من بوده یا چیز دیگه ای ؟ اگه ارسال نشده دوباره بپرسم در مورد دکتری 96 هست
- حامد
e^z=e^x .e^iy
اگر x به سمت بی نهایت میل کند ،مقدار حد بی نهایت است،اما اگر روی مسیر y به سمت بی نهایت حد بگیریم lim e^iy وجود ندارد.
موفق باشید
- آتنا
- amir
https://goo.gl/PBfsDI
- pooriya
- آرش
سوال سال 92 مهندسی نفت که تابع درون انتگرال به شکل z+2/z هست رو چرا نمیشه با فرمول کوشی حل کرد در حالی که فقط توی صفر غیر تحلیلی هست و 2pi که با فرمول کوشی بدست میاد فقط بخشی از جوابش هست ؟؟؟
سوال بعدیم اینکه که چطوری سریع تشخیص بدیم که انگرال غیر تحلیلی است و باید از تغییر متغیر به روش t حل کنیم و یا با انتگرال کوشی و غیر تحلیلی بودن تو نقاط خاص؟
برای تشخیص سریع توابع غیرتحلیلی معروف بهتر است درسنامه دوم (توابع مختلط) فصل اول را یکبار دیگر مرور کنید تا در برخورد با توابع مختلف نقاط غیرتحلیلی آن ها را به سرعت به یاد بیاورید.برای استفاده از انتگرال کوشی نیز به تعریف آن و اینکه شروط تعریف رعایت شده باشد باید دقت کرد.
- سامان
در مورد معادلات ناهمگن سوال داشتم. من درسنامه ی مشتقات کتاب رو خوندم. فایل های جدیدی هم که تو سایت قرار دادین خوندم. ولی الان که به صورت جامع تست میزنم و بایک معادله ی ناهمگن برخورد میکنم نمیدونم از روش ضربی برم یا لاپلاس یا از روش u=w+v . لطفا یک الگوریتم در مورد حل این سوالات به صورت خلاصه اگه توسایت قرار بدین خیلی میتونه کمک کننده باشه. چون درسنامه های هر بخش جداست به صورت جامع یکم سخته.
لطفا راهنمایی کنید که چطوری میتونم حل کنم
باتشکر
2-به هر حال بعد از تغییر متغییر u=w+v باید ضابطه v(x,t) از روش ضربی به دست بیاید،اما در تست ها فقط انجام تغییر متغیر را می خواهند
3-برای لاپلاس فقط وقتی اقدام کنید که معادله نامتناهی یا نیمه متناهی باشد و شرایط مرزی و اولیه هم تبدیل لاپلاس را مشکل نکنند.در ضمن اگر گزینه ها یا معادله شامل توابع پله یا ضربه هستند یا جواب دو ضابطه ای است حدس می زنیم لاپلاس بهتر باشد.
موفق باشید
- آرش
ممنون.
- pooriya
ببخشید توی درسنامه سوم از فصل چهارم( محاسبه انتگرال مختلط با کمک مانده ها) چندین مثال متوالی توضیح اظافی دادین که چون تابع داده شده زوج هستش و نقاط تکین این توابع زوج قرینه هم هستن؛ پس از همون اول میشه گفت که حاصل انتگرال مختلط اونها برابر صفر هستش.... می خواستم بدونم که چجوری میشه راحت فهمید که تابعی زوج هستش یا فرد....؟ البته توابعی مثل sin ,cos و که معلومه ولی مثلا مثال 11 یا 18 چجوری فهمیدین که تابع زوجه؟؟؟
cos زوج است و sin فرد.
کافیست به جای z ها -z بگذارید و خاصیت زوج و فرد بودن را در هرتابع بررسی کنید.
- Saji
در صفحه ۵۳ کتاب ریاضی مهندسی چاپ ۹۴ مثال ۱۱
در حل این مثال برای اثبات برقراری روابط کوشی ریمان برای تابع g اومدید از u و v مشتق گرفتید سوالم در مورد مشتق گیری ها بود. برای مشتقگیری لیمیت گرفتید ولی عبارت داخل لیمیت صفر صفرم میشه و بدون اینکه هوپیتال استفاده کنید جواب رو قرار دادید صفر چطوری این مشتق هارو حساب کردید؟ یعنی مشتق u نسبت به x و بقیه مشتقات چطوری صفر شدند؟! ممنون می شوم توصیح دهید.
با سپاس
- مائده
- آرش
توی جل معادلات به روش ضربی مثل مثالی که در صفحه 530 زده شده (اولین مثال حل معادله به روش ضری 3 گام) شما ضریب 2 رو که همون c در معادلات موج هست به مخرج gt بردین در حالی که میشد مثلا تو صورت ft قرارش داد و مسئلرو حل کرد. سوال من اینه ضرایب رو واسه کدوم معادله لحاظ کنیم آیا فرقی داره ؟ و روش تشخیص چیست .
ممنون.
- امیرحسین
در درسنامه پنجم اولین مثال شما فرمودید که تابع w را تابعی از x در نظر میگیریم لطفا دلیلش رو توضیح میدید
در صورتی که در فرمول کلی تغییر متغیر w به این صورت (x,t) آمده
- pooriya
استاد در فصل چهارم توی درسنامه 1 توی مثال های اولیه شعاع سری توانی به مشکل خوردم...مفهومی نیست محاسباتیه... گفتم ادامه ندم اول بپرسم... توی مثال 1 چجوری حاصل حد به e^-1 رسید؟؟؟ همینطور در مثال 2 میشه نحوه ساده سازی و باز شدن عبارت های فاکتوریل رو یه توضیح بدین...
ممنون
در مثال 2 فاکتوریل ها را باز کتید جملات صورت و مخرج ساده می شوند.موفق باشید
- pooriya
- آرش
ممنون.
- م
2سوال داشتم
1-منظور از هارمونیک چیست ؟ و هارمونیک زوج و فرد یعنی چه؟
2-چگونه در مثال 20 تشخیص بدهیم هارمونیک فرد مدنظر است؟ درست است از روی بازه ی n که فرد است تشخیص دهیم یا موردی دیگر است؟
و شکل تابع را چگونه رسم کردید؟
با تشکر
- آرش
این بخش جدید از درسنامه یک مقدار حفظیه خواستم ببینم با توجه به مطالبی که قبل از این بیان شده میتوان به سوالات نا همگن به صورت کامل پاسخ داد و این مبحث رو نخونیم ؟
- آرش
در حل معادلات ناهمگن با شرایط هگن چه موقع بفهمیم باید از تفیک متغیرها حل بشه و چه موقع بفهمیم باید تغییر متغیر گرفته بشه ؟ مثل سال 94 که با روش ضربی راحت حل میشد.
در همگن کردن شرایط مرزی نا همگن میتونیم برای سرعت عمل از همون اول شکل کلی یک تابع خطی رو بصورن ax+b بنویسیم و شرایط رو چک کنیم و فقط در حالتی که شرایط ناهمگن هردو روی ux بود به صورت ax^2 + bx + c در نظر بگیریم ؟
اگر تابع ناهمگن در صورت سوال بر حسب t بود تغییر متغیر باید فقط بر حسب t باشد ؟
ممنون.
- آرش
وقتی کمان درون سینوس یا کسینوس مثلا در میاد np به اضافه یک مقداری چطوری باید علامت رو بفهمیم من گیج میشم ! و اگه np به علاوه یا منهای p/2 باشه چطوری علامت رو تعیین کنیم با توجه به اینکه نسبت هم عوض میشه ؟
عموما تو معادلات با مشتقات جزیی و سری فوریه به این حالتها زیاد برخورد میکنیم.
- آرش
تو روش تفکیک متغیرها و روش کلی در اکثر مواقع لاندا 0 و مثبت به جواب نمیرسه و اغلب لاندا منفی مطلوب ماست و در شرایط مرزی صدق میکنه ! میتونیم واسه افزایش سرعت عمل فقط این شرط رو لحاظ کنیم در مساعل ؟ و استثناعاتی وجود داره که حتما لاندا 0 و مثبت رو چک کنیم ؟
ممنون.
- امیرحسین
من با اینکه مبحث های دیگه کتابتون مثلا فوریه یا هرجای دیگه رو خیلی خوب متوجه شدم
اما واقعا نمیدونم چرا تو مبحث مشتقات جزیی نمیتونم پیشروی کنم
حاظرم هر جزوه یا چیزی که شما به دلیل تجربه زیادتون پیشنهاد کنید رو تهیه کنم با هر مبلغی
فقط لطفا یه پیشنهاد اثر بخش بدین(اگه ممکنه جوابو بهم ایمیل کنید)
- آرش
توی بخش میله متناهی و نیمه متناهی فرمولهایی وجود داره که حفظیه و روش اثباتشم کامل توضیح ندادین و ازونجایی که حفظ کردنشونم تقریبا غیر ممکنه ! راه حل چیست ؟ جایی اثباتشون وجود داره که بخونیم ؟
- آرش
تمام تغییرات چاپ 20 و 21 نسبت به 22 همین 2 درسنامه و همون بخش سری فوریه هست ؟
- آرش
پیرو درخواست قبلی منظورم اینبود مثل رابطه تعمیم یافته سری فوریه برای ضرب دو تابع که واسم ارسال کردین اگه مطلبی مرتبط با سوالات مشتقات جزئی در کنکور 95 برق وجود داره و مهمه و تازه به کتاب اضافه شده اگه امکانش هست واسم ارسال کنید.
با تشکر.
goo.gl/xZQUwW
- pooriya
- pooriya
ممنون
"در ضمن استاد من اون فلوچارت رو هم که به عنوان خلاصه درسنامه سوم گذاشتین رو خوندم"
به محض اینکه از خط x=y خارج می شویم شرط کوشی ریمان برقرار نیست بنابراین مشتق پذیر و تحلیلی نیست.
شما چاپ چندم کتاب ریاضی مهندسی را مطالعه می کنید؟
- آرش
میشه خواهش کنم اگه مطلب جزیی در این مبحث مرتبط با سوالات کنکور 95 دارین واسم ارسال کنید ؟ یک دنیا ممنون.
- حسین
- Saji
ابتدا باید از نگارش بخش حل سوالات بدون دخالت دست !! تشکر بکنم بخصوص بخش مربوط به فصل شش خیلی جالب بود. بنده داوطلب دکتری رشته مکانیک گرایش تبدیل انرژی هستم.
بنابه توصیه حضرت عالی بنده (سوالی که قبلا در سایت پرسیده بودم) بنده فصل های پنج و شش کتاب ریاضی مهندسی رو مطالعه کردم و تست های تالیفی رو هم یک در میان حل کردم و قسمت های رد گزینه تمام فصول کتاب رو هم مطالعه کردم البته همه سوالاتشون رو حل نکردم از بحث های مختلط هم فقط نگاشت یعنی فصل دو رو مطالعه کردم و گذرا فصل یک رو مرور کردم ولی فصل سوم یعنی انتگرال مختلط رو کلا مطالعه نکردم و پیشینه خوبی هم از این فصل ندارم. حالا سوالم از خدمتتون اینه که بنظرتون در زمان باقیمانده من فصل سه رو هم مطالعه کنم یا اینکه این زمان رو اختصاص بدم به بقیه فصل هایی که مطالعه کردم و همه سوالات تالیفی رو پوشش بدم؟ و اینکه آیا لازم هست همه سوالات بخش رد گزینه رو حل کنم چون احساس میکنم روند کلی رو یاد گرفتم
با سپاس فراوان
- امیرحسین
چاپ بیستو یک فصل پنجم صفحه ۴۳۱ تست نهم
چرا برای محاسبه انتگرال f قبل انتگرال (1/2π( گذاشتید مگه L ما π نیست؟
- pooriya
حاصل مجموع=یک منهای (iz-) به توان 6 بر روی یک منهای (iz-).حالا مشابه تست 34 حل می شود.
- آرش
با تشکر از لطف زیادتون که پاسخ رو واسم ارسال کردین.
در مورد سوالتون بنده پارسال کنکور دادم ریاضی مهندسیرو بارها و بارها خوندم مسلط شدم به تمامی تستها مخصوصا کنکور اما یسری جاهارو متاسفانه سطحی گذر کردم ! این رابطه تعمیم یافته پارسوال که متاسفانه تو کتاب نبود منم بلد نبودم علارقم سادگی سوال.
سوالهای 36 و 37 رو علارقم تسلط کامل به فصل مشتقات جزیی نتونستم حل کنم و انتگرال سوال 41 که فکر میکنم از درسنامه 4 فصل 4 مطرح شد که متاسفانه از سرفصل (محاسبه ی نوعی دیگر از انتگرالهای حقیقی) بدلیل سنگین بودن مبحث و احتمال کمی که واسه اومدن سوال میدادم مطالعه نکردم.واسه همین یه نگاهی به سوالای پارسال انداختم تا ببینم مشکلم چی بوده.خواهش عاجزانه ای که دارم اگر ویرایش جدید کتاب تعداد انگشت شماری مثال متناسب با کنکور 95 افزوده شده در اختیارم بزارین تا نخوام هزینه زیادی رو واسه چاپ جدید کتابی که همین پارسال تهیه کردم بدم. لطفتون رو فراموش نمیکنم.
با تشکر فراوان
- Galaxy021
- Galaxy021
با تشکر
- Galaxy021
1- استاد یه ابهام واسم پیش اومده تو این سوال مگه نه اینکه ما باید مانده رو تو نقطه شاخه ایLn هم که از برابر صفر گذاشتن ارگومانبه رو بدست میاد و اینجا z=1/2 هست پس چرا تو پاسخ طراح از این قضیه صرف نظر کرده؟؟؟
2-با اینکه یه مشترکاتی هم بین تعاریف تحلیلی و همساز وجود داره اما شما تو تعریف همساز گفتید تابعی که تحلیلیه همسازم هست چرا؟؟ اصلا میشه مرزای دقیق بین اینا رو مشخص کنید.
http://s8.picofile.com/file/8280871176/2017_01_01_23_26_37.png
http://s8.picofile.com/file/8280871284/2017_01_01_23_27_13.png
با تشکر
- امیرحسین
من سوال 11 از تست های تکمیلی فصل چهار صفحه 351 چاپ 21 رو نمیتونم حل کنم لطفا راهمایی یا حل کنید
متشکر از اینهمه انرژی و وقتی که میذارید
- آرش
- محمود
استاد سوالمو براتون ایمیل کردم بسیار ممنون میشم اگه بررسی بفرمایید
باتشکر
- محمدامین عرب
در صفحه پنجاه و چهار کتاب ریاضی مهندسی یکی از راه های بررسی برقراری شرط کوشی ریمان صفر شدن مشتق تابع نسبت به زد بار بیان شده.
اما در مثال هفده صفحه پنجاه و شش راه حل ارائه شده متناقض با این فرمول به نظر می رسد. چگونه می توان توجیه کرد؟
پیشاپیش متشکرم
- سجاد
۱- آیا لزوما باید کتاب از ابتدا به انتها خوانده شود آیا در فصول انتهایی کتاب از مطالب عنوان شده در فصول اول استفاده می شود یا اینکه میتوان هر فصل را جداگانه با توجه به علاقه مطالعه کرد؟
۲- با توجه به اینکه زمان محدودی تا برگزاری آزمون دکتری باقی مانده است، با توجه به سابقه خود، کدام فصول را برای آزمون دکتری مهندسی مکانیگ گرایش تبدیل انرژی دارای اولویت میدانید؟
- Galaxy021
مثال ۱۴ رو طبق سیگنال چرا به راست شیفت ندادید؟؟خب اینجام در نهایت میره تو پرانتز چرا پایین نبردید؟طبق توضیحاتتون باید پایین برد اما تو حل بردید به راست چرا؟
- امیرحسین
در فصل 5 درسنامه اول از قسمت تست های پایان درسنامه صفحه 400 سوال 45
چرا این سوال a0 ندارد مگر تابع ما فرد است؟
با تشکر از زحماتتان
- افشین رحمانی نژاد
احتراما:
1-آیا میتوان در سوالاتی که بخشی از تابع زیر انتگرال دارای نفاط تکین شاخه ای
هستندنقاط تکین را بدون بررسی که در ناحیه بسته cقرار میگیرد یا نمیگیرد
صرفنظر کنیم که در زمان صرفه جویی شود یا اگر خیر چگونه میتوان مانده نقاط تکین شاخه ای درون مرزcرامحاسبه کرد.
2-رابطه آرک کوتانژانتzبکاررفته در حل مثال 38 یک منها با رابطه4 تعریف
آرک کوتانژانت z ص38 متفاوت است.البته فکر کنم رابطه4ص38درست باشد چون هردوپاسخ در گزینه ها موجود است.ممنون
- مهدی
- افشین رحمانی نژاد
این مثال سوال بسیار اموزنده و حرفه ای از 2 مبحث نگاشت و انتگرال هست.
سوال 1:آیا این مثال تا به حال جزو سوالات ارشد سالهای قبلی بوده یا نه؟اگرخیر بفرمادید احتمال مطرح شدن اینگونه سوالات ترکیبی در کنکور ارشد هست یا خیر؟
سوال دوم:نفهمیدم که نقطه تکینi/2 ∏ چگونه در داخل دایره IzI=√2
افتاد.رادیکال2 دایره ای به مرکز مبدا وشعاع تقریبی 1.4 است ولی نقطه
تکین2/∏باید جایی حدود 1.57i باشد.لطفا توضیح بفرمائید.
باتشکر فراوان
- افشین رحمانی نژاد
استادلطفابفرمائید در محاسبات کجا اشتباه میکنم لینک ارسالی به شرح ذیل
است. http://s9.picofile.com/file/8271815692/Image_17_.jpg
- Galaxy
استاد اينو ميدونم اما علت حرکت عکس چيه که t+1 یعنی یکی به چپ؟! مگه زمان یک واد افزایش پیدا نکرده؟؟!
- Galaxy
چرا (X(2t سیگنال رو دو برابر جمع میکنه در حالی که زمان دو برابر شده؟! یا چرا(X(t/2 سیگنال رو دو برابر میکنه در حالی که زمان نصف شده؟! استاد خواهش میکنم کمکم کنید يه پارادوکس که هر کاری میکنم جوابی واسش پیدا نميدونم
با تشکر
- majid
استاد یه سوال داشتم که لینکشو براتون فرستادم http://s9.picofile.com/file/8270052600/IMG_20160923_180834.jpg
درپناه خدا
- رسول احمدی
- رسول احمدی
- افشین رحمانی نژاد
بنده این مثال را با نگاشت w=az b حل میکنم به پاسخ گزینه 2 میرسم لطفا توضیح بفرمائید
با تشکر فراوان
- افشین رحمانی نژاد
اگر نخواهیم جای z را با w عوض کنیم وبا همان نگاشتw=az+bحل کنیم
به پاسخ 2 میرسیم لطفاتوضیح بفرمائید
متشکرم
- Galaxy
http://s8.picofile.com/file/8268072650/DSC_0985.JPG
- Galaxy
- Galaxy
***استاد شما گفتید فرم پاسخ ویژه همونه اما تو درس معادلات جواب ویژه ناشی از معادله اشتروم-لیوویل هستش که اونم یه معاله همگنه اما اینجا این معادله رو نداریم که پاسخاش موهومی دراد و ادامه قضیه از طرفیآرگومان پاسخ میشد مقادیر ویژه که با شرایط مرزی تعیین میشدن اینجا با کدوم شرط مرزی آرگومانا یک شدن؟
***با استدلال مداری میشه توجیه کرد؟ میگفتیم پاسخ شبیه ورودی هست و اینجا چون سمت راست ورودی سینوسی بر حسب ط هست پس جواب به فرم مذکوره؟
بله از نظر مداری هم همین معنا را دارد.
- Galaxy
با تشکر
http://s9.picofile.com/file/8268032568/DSC_0984.JPG
- Galaxy
- Galaxy
1-تو مثال 8 ص 638 چاپ بیستم چرا گفتید شکل کلی Up=A(s)sinx+B(s)cox هست؟ چرا طور دیگه ای نیست؟ چرا آرگومانا بر حسب x هستن و برحسب مثلا t نیستن؟ چرا ضریب x تو آرگومان1 هست و عدد دیگه ای نیست؟
2-چرا ضرایب فوریه معکوس سینوسی و کسینوسی ص 640 با ضریاب نظیرشون تو بحث تبدیل فوریه ص 456 تو یه رادیکال فرق دارن؟
3-روابط فوریه سینوسی و کسینوسی که برای Uxx نوشتید چطور اثبات میشن و بدست میان؟
4-تو مثال 10 ص 639 دلیل اینکه چرا تو فوریه معکوس 1/2p وجود داره رو میشه منطقی تر و مستند تر بیشتر توضیح بدید؟
1:این مربوط به درس معادلات دیفرانسیل است .فرم کلی جواب ویژه به صورت:yp=asinbx+dcosbx است
2:در بحث ضریب تبدیل فوریه منابع مختلف به شکل متفاوتی عمل می کنند.اگر در تعریف f^(w) ضریب رادیکال 2 بر روی Π را استفاده کنند در تعریف f(x) هم رادیکال 2 بر روی Π در نظر می گیرند.اما برخی منابع یکی از فرمول ها را با ضریب 1 و دیگری را با2 بر روی Π می نویسند.ضریب فوریه در حل مسایل مربوط به آن نقش مهمی ندارد و در تست های کنکور طراح سوال تعریف مورد نظرش را مشخص می کند.(اما حالت کلی را برایتان ایمیل شد.)
3:با مشتق گیری نسبت به x از طرفین تبدیل فوریه.
4:به توضیحات سوال 2 مراجعه کنید.
- Galaxy
- مهدی
- امیرحسین
تو فصل نگاشت ، مسائل آخر فصل سوال 83 (صفحه 134) نگاشت
ln((z-1)/(z+1)
را می توان به داخل دایره واحد تصویر کرد و ....
اما شما از روش دیگه رفتید که جواب ها یکسان نمیشوند ؟ لطفا توضیح بدید متشکر
- Galaxy
با تشکر
- محمود
استاد چند روز پیش سوالی پرسیده بودم،اگه امکانش هست بررسی بفرمایید
باتشکر
- Galaxy
اینم لینکاشونه
http://s2.picofile.com/file/8265348034/1.jpg
http://s2.picofile.com/file/8265348126/2.jpg
http://s1.picofile.com/file/8265348300/3.jpg
http://s2.picofile.com/file/8265348518/4.jpg
http://s2.picofile.com/file/8265348600/5.jpg
http://s1.picofile.com/file/8265348768/6.jpg
با تشکر
در پناه حق تعالی
- سعید
http://s2.picofile.com/file/8265147076/%D8%B2%D8%B1%D8%B0%D8%B2%D8%B1%D8%B0%D8%B2%D8%B1%D8%B0%D8%B2%D8%B1%D8%B0.jpg
ممنون
- افشین رحمانی نژاد
لطفا توضیح بفرمائیدچرا در مثالهای 8ص205و10ص206به خاطر منفی بودنn
در توان سری از نوع سری توانی لحاظ نشده(ازراه سری تابعی حل شده) اما درحل مسائل 6و10ص223 از راه حل سری توانی حل شده است؟
- امیرحسین
تو صفحه ی 40 کتاب سوال 12 و 13 دو تا سوال تقریبا شبیه هم هست ولی هر دو با دوتا روش مختلف حل شده(هر دو روشم درسته)
که
یکی رو با اونیکی روش حل می کنم به جواب نمیرسم
لطفا بگید چکار کنم
- افشین رحمانی نژاد
لطفا توضیح بفرمائیدچرا در مثالهای 8ص205و10ص206به خاطر منفی بودنn
در توان سری از نوع سری توانی لحاظ نشده اما درحل مسائل 6و10ص223 از راه حل سری توانی حل شده است؟
یک بر روی w را داریم که توانی است.شعاع همگرایی را که حساب کردیم |w| کوچکتر از 1/2 پس 1 بر روی |z-1| و جواب به دست می آید.در مثال های 8صفحه 205و10صفحه 206 هم می توانیم همین کار را به صورت مشابه انجام دهیم.
- سعید
سؤال اول : اینکه نگاشت همدیس و همانی را تحت دو عنوان معرفی کردین ، حتمأ بین اونها تفاوت هایی وجود داره ... چه تفاوتی بین این دو وجود داره؟یا اینکه هردو دقیقأ یکی هستند؟
سؤال دوم:صفحه 102 - کادر آبی رنگ وسط صفحه شماره 1 - آخرش فرمودین : "...خطی که از مبدأ عبور میکند، تبدیل می شود"
این " میکند " که در آخر جمله اومده ، نباید به " نمیکند " تبدیل بشه؟
منظورم اینه که اشتباه تایپی صورت نگرفته؟
در مورد سوال دوم ،خیر اشتباه تایپی رخ نداده است.البته واضح است که در نگاشت w=1/z هیچ گاه w به صورت مطلق صفر نمی شود اما وقتی که z به سمت بینهایت میل کند خواهیم داشت w به سمت بی نهایت میل خواهد کرد.برای مثال خط y=x توسط این نگاشت به خط v=-u تبدیل می شود.
- سعید
http://s2.picofile.com/file/8263629718/Scan2.jpg
ممنون
در مورد مثال 8:محاسبه ux,uy,vx.vy در همه نقاط وقت گیر است به همین علت از تعریف مشتق استفاده کردیم تا سریعتر متوجه وجود یا عدم وجود مشتق شویم.
در مورد مثال 9:چون ux,uy,vx.vy از چندجمله ای ها تشکیل شده اند و پیوسته بودن چندجمله ای ها واضح است نیازی به بررسی آن نداشتیم.چند جمله ای هایی مثل x+y یا x^2-xy یا توابعی مثل sinx,cosx ,e^x به وضوح پیوسته هستند.
- سعید
سؤالم رو در لینک زیر آپلود کردم.
http://s1.picofile.com/file/8263628000/Scan1.jpg
ممنون
- سامان
پی به توان 2 منهای پی چطوری حساب شده؟اون منها از کجا اومده؟
ممنون
- سامان
در جواب این تست آمده که گزینه 4 صحیح است و دارای بسط فوریه نمی باشد
اما در نکته 4 ص 379 فرمودید به ازای هر aبزرگتر از صفر پیوسته است و در فاصله ی منفی ال تا مثبت ال سری فوریه دارد.طبق این نکته تست دارای سری فوریه هست. لطفا این مورد رو توضیح بدین. باتشکر
- Galaxy
استاد نگاشت ناحیه y از منفی یک تا یک , x از منفی پای دوم تا پای دوم تحت w=cosz رو با استفاده از بسط و تعیین علامت چطور بدست بیارم؟ مرز به مرز نه استاد اونو بلدم.
با تشکر
- Galaxy
با تشکر
- محمود
استاد میخواستم درمورد نحوه ی مطالعه راهنماییم بفرمایید،باتوجه به اینکه از فصل 4و6 کتاب هیچی نمیدونم خوندنش خیلی برام سخت شده الان ک فصل چهارم خیلی کند پیش میرم و بیشتر سوالارم بار اول نمیتونم حل کنم.من خیلی ضعیفم یا اساسأ سوالا خیلی قوی طرح شدند؟
ب نظرتون همین طور پیش برم تا دور دوم عمیق شم و از خودم انتظار داشته باشم ک بتونم حل کنم...؟
باتشکر
- Galaxy
با تشکر
- وحید بسیم
sin(Π/2-Π/8)=-cos(Π/8)-:بنابراین
- محمود
استاد در فرمول انتگرال کوشی صفحه180 اگر z مخرج ضریب داشت باید فاکتور بگیریم بیاریمش بیرون یامیشه همینجوری مساوی صفر قرار بدیمو ریشه رو بدست بیاریم؟
استاد بسیار بسیار ممنون میشم اگه کارنامه رتبه های برتر امسال روبذارید
باتشکر
در اولین فرصت حتما بر روی سایت قرار می گیرد.موفق باشید
- م
استاد شما اطلاع دارید که آخرین چاپ کتاب های سیگنال و مغناطیس و کنترل خطی احتمال الکترونیک 1و2 مدرسان شریف چه شماره ای ست؟ اگر اطلاع ندارید از کجا باید بپرسم؟ کتاب ریاضی مهندسی آخرین چاپش 21 است؟ با سپاس از شما
- ahmad
ببخشید تو صفحه ی ۴ از کتاب قسمت ضرب خارجی دو عدد مختلط برای محاسبه ی زاویه ی بین دو بردار مختلط از طریق سینوس باید اندازه ضرب خارجی تقسیم بر ضرب اندازه هاشون بشه ولی تو کتاب اندازه ها رو لحاظ نکرد
مثال ۳۶ (ص ۱۲ کتاب) برای xها دو مقدار به دست اومده ولی تنها یکی از zها رو که از روی xها به دست میان لحاظ کرده
ممنون
- سعید
اول اینکه خیلی خیلی ممنون بابت اینکه به سؤالات ما جواب میدین
سؤالم رو در لینک زیر قرار دادم
http://s2.picofile.com/file/8260500476/riyazi_mohandesi.jpg
ممنون
- افشین رحمانی نژاد
با توجه به اینکه زاویه شکل با سطح افقی3/pاست نگاشت مرحله دوم
(w2) اشتباها6/p درنظر گرفته شده که نتیجتا گزینه چهارم پاسخ درست معرفی
شده در حالیکه گزینه 2 درست در میاید.لطفا اگر درست است تائید بفرمائید.
- سامان
چطوری از سیگمای یک بر z به توان n+1 انتگرال گرفته که ln ظاهر شده
انتگرال گیری رو متوجه نشدم.
lnz ظاهر می شود.
- سامان
در جواب فرمودین لااقل یک m منفی am مخالف صفر باشد. دلیلش چیه؟
اگر صفر نباشد چرا تکین تنها نمیشود؟
- سامان
استاد من این سوال را حل کردم مانده منفی پی دوم ( p/2 ) میشود چون اگر
Z-p/2 را t بگیریم و t را به صفر میل دهیم مانده برابر منفی پی دوم میشود . آیا من اشتباه کردم ؟
- افشین رحمانی نژاد
در مورد تست 34 ارشد95که خواستاررابطه بازگشتی معادله بسل مرتبه اول
(با لاندابرابر 1)است جنابعالی گزینه 4 و سازمان سنجش گزینه 1 را صحیح اعلام
کرده است. اما با توجه به رابطه بازگشتی مندرج در صفحه 354کتاب ریاضی مهندسی مدرسان شریفan=(-1)an-2/n(n 2λ) باید به رابطه ای شبیه بهan=(-1)an-1/n(n 2) برسیم که در هیچ گزینه نیست.
- سامان
سوالات تکمیلی فقط پاسخنامه ی کلیدیش تو سایته؟
پاسخنامه تشریحی رو نمیذارین؟
- محمود
استاد ببخشید من هنوز متوجه نشدم،
اگر لگاریتم شاخه اصلی باشه که فرمول ln(a^2)=2lna برقرار نیست درسته،پس با این اوصاف اتفاقا توابع توانی رو در صورتی میشه تعریف کرد ک ln شاخه اصلی نباشه(arg محدود نشده باشه).(گذشته از چند مقداری شدنش).این طور نیست؟
با تشکر
- محمود
استادطبق گفته کتاب اگر آرگومان رو محدود کنیم تا فقط روی یک شاخه باشیم ln خوش تعریف میشه ولی ب جاش دیگه فرمول ln(a^2)=2lna برقرار نیست،پس با این وجود چرا اجازه داریم توابع توانی رو ب صورت صفحه35 تعریف کنیم مگه تو این فرمول از رابطه بالا استفاده نشده؟
با تشکر
- پیمان پازوکی
در صفحه 33 همین کتاب در مثال 7 گزینه 4 به روش دیگه ای حل کردین.
ممنون میشم اگر جواب درست را بدهید. با تشکر
مثال 7 هم روش دیگری نیست همان فرمول کلی است.موفق باشید
- آرش
برای محاسبه ی مانده از فرمول تکین مرتبه اول با مشتق گیری به جواب ذکر شده توی کتاب میرسیم ولی با استفاده از فرمولیا نتگرال کوشی مانده در z=3/2 برابر 2/3 میشه نه 1/3 ایراد کار کجاست ؟
در فرمول انتگرال كوشي مخرج بايد z-z0 باشد. اگر z ضريب دارد اول بايد از ضريب z در مخرج فاكتور بگيريد. اين كار را انجام دهيد درست مي شود.
- ناصری
- آرش
ببخشید زوج و فردیو مگه با تبدیل w به -w چک نمیکنیم ؟ خوب تو گزینهای 1 تا 3 ام که فرده ولی شما نوشتین فرد نیس ! حقیقی و موهومی بودنم با شرط تقارن هرمیتی چک میکنیم درسته ؟
مرسی
- آرش
توی سوالاتی که مثلا sin یا cos در بسط فوریه یک تابع مثلا x صرب میشه و از ما xsinx رو میخواد روش حل چطوریه ؟
با تشکر.
- محمود
صفحه16 گفتید اگر z ریشه باشه مزدوجش هم ریشه است،ولی تو مثال 26 صفحه 9 اینطور نشده دلیلش چیه؟
قصد ندارید برای معادلات دیفرانسیل معمولی کتاب بنویسید؟اگه خواهش کنیم چی؟
به دلیل مشغله های فراوانی که دارم فعلا فرصتش نیست،انشالله در اولین وقتی که پیدا کنم این کار را خواهم کرد.موفق باشید
- راضیه یاراحمدی
ببخشید درسنامه 7فصل ششم ریاضی مهندسی صفحه649مثال 4بعداز بدست اوردن r=y+2xاز روی چی این رند ها حساب شده ک جواب شده 2urr+2urs
میشه لطف کنین بگین چطور واز روی چی اینارو نوشتین ممنون میشم
- آرش
ببخشید من حسابی تو این سوال گیج شدم با توحه اینکه هیچکدوم از جوابای توی اینترنت با اونیکی نمیخونه! مثلا تو جواب شما مگه بعد از مشتق گیری از سری توانی کران سیگما یکی اضافه نمیشه ؟ و برای دفه بعد یکی دیگه ؟ که بعد باید حملات اضافیرئ بکشیم بیرون ؟ بعد تغییر ن=توان تو ضرایب و شماره جملات جلوی سیگما همزمان اثر میزاره دیکه ؟
- آرش
با رسم شکل تابع دیده میشه که نسبت به نصف L تقارن زوج داریم پس چطوری از روش تشریحی به ضرایب فرد رسیدیم ؟ مگه فقط وقتی تقارن فرد داریم (نیم موج) ضرایب فرد نمیشه ؟
- آرش
توی این مسعله فقط میتونیم از فرمول بریم ؟ یعنی بخاطر اینکه تو زاویه 0 یا p نمیتونیم مقداری به معدله بدیم نمیشه از فرم معادله پواسون مستقل از r حل کنیم ؟
با تشکر.
- آرش
ببخشید تو پاسخی که دکتر شفیعی گذاشتن برای ریاضی مهندسی واسه سوال آخر ذکر کردن که چون با انتگرال گیری سری فوریه کسینوسی میشود پس مقدار ثابت کمتر از 1 داریم میشه لطفا در این مورد توضیح بدید من متوچه نشدم !
با تشکر.
- آرش
- 95
و خسته نباشید.
از اینکه وقت خود را به بنده اختصاص دادید تشکر میکنم.
شاد و سلامت باشید
- آرش
مرسی از جوابتون من منتظر میمونم ! عیدتونم مبارک باشه برای ماهم دعا کنید مرسی :)
- آرش
ببخشید من با روش حل دالامبر هیچ مشکلی ندارم جز قسمته آخرش که باید محدوده رو تعیین کنیم نمیدونم باید چه مقداری رو کم کنم یا اضافه کنم !
ممنون میشم راه حلی اراعه بدین کی باید کم کنم ضرایب دوره تناوب و چه زمان اضافه کنم به مقدار درون تابع ! (آیا زوج یا فرد بودن گسترش به این بخش از حل ربط داره ؟ ) مرسی
- آرش
صفحه 649 مثال 60 به جواب 4 رسیدین ولی توی حل تشریحی گفتین که سری فوریه دوگانه فقط وقتی مقدار ثابت داره که هر دو جمله کسینوسی باشند پس گزینه 2 درسته ؟
- آرش
ببخشید امکانش هست پاسخ تشریحی ریاضی و مدار دکتری 95 رو بزارین ؟ فکنم خیلی مفید باشه برای ارشد 95 .
ممنون از لطفتون.
- 95
یک به روی z-1 کلا ضربدر sin1/z در ناحیه z=2 چرا با وجود اینکه z=1و z=0 داخل ناحیه هستند همچنان بصورت بسط لوران mz نوشته میشود؟
- 95
ببخشید یه سوال بدجور گیجم کرده اگر کمک کنید لطف بزرگی نمودید.
ما در بحث بسط لوران اگر یه کسر داشتیم و بازه را مشخص کرده بود ابتدا میومدیم نقاط تکین رو بدست می اوردیم و اگر داخل بازه بود با قدر نسب m/z و اگر خارج بود با قدر نسب mz مینوشتیم و بسط میدادیم .اما در سوال زیر من نمیدونم این موضوع رو چرا پیاده نکرده
z تقسیم بر z+1 کلا ضربدر e^1/z اگر ناحیه اندازه z=1 باشد.
- آرش
سلام
روش اصلیه حل این سوالا چطوریه ؟ که تو فرم اصلیه معادلات موج حرارت و پواسون نیستن ؟
با تشکر
- آرش
من کل ریاضیو خوندم ولی متاسفانه تو این بخش به مشکل خردم ممنون میشم کمکم کنید . اول شکل کانونیک معادلات که با زتا و ... نشون دادید توی صفحه 648 نمیفهمم.اولین مثالی که متوجه نمیشم مثال 4 .
با تغییر متغیرهای انتخاب شده مشکلی ندارم.
ازونجایی که بادی ux و uy رو بر حسب تغییر متغیرها بنویسیم مشکل دارم و گیج میشم ! مثلا تو بخش اول میشه گفت ux رو برحسب تغیر متغیری گسترش دادیم که x داره درسته ؟ حالا تو بخش بودم یعنی uy اونحایی که گسترش شامل du/dr شده اصلا متوجه نمیشم چطوری تشکیل شده ! ممنون میشم بیشتر توضیح بدید.
- آرش
سلام
ببخشید بخش دوم این سوال که x ,y رو برحسب u و v نوشتید رو متوجه نشدم ضمن اینکه روش اصلی حل نکاشت برای اینگونه سوالایی که ضابطه داره چیه و یا خط داده میشه مثلا تو این سوال صرفا خط به خط با فاز مخالف تبدیل میشه و نمیشه با نقطه گذاری کاری کرد. ممنون
- آرش
ممنون.
- حميد
استاد کشی ریمان رو از طریق تعریف مشتق بررسی کرردید.
میشه در مورد این روش توضیح بدید؟
- آرش
پیرو پست قبلیم باید بگم من معادلاتو مطالعه کردم ولی ازونجا که نگارش کتابه ریاضی مهندسیتون خیلی به دلم نشست واقعا دوست داشتم رد کزینه معدلاتم بخونم آخه هیچ تکنیکی تو این ضمینه بلد نیستم متاسفانه. شما منو به ریاضی مهندسی علاقه مند کردید در حالی ضعیفترین درسم بود توی کنکور امثال به قویترین درسم تبدیل شده مرسی از زحماتتون که میدونم خیلی وقت برده نوشتنه این کتاب :)
- احسان
در روش ضربی معیار ثابتی که برابر اون قرار میدید چیه
مثلا گاهی k
گاهی لاندا گاهی لاندا به توان 2
بر اساس چه معیاری قرار داده میشه؟؟؟
ممنون ازتون
- معصومه سادات بنی جمالی
استاد صفحه 547کتاب شما مثال 9
1-طبق متن درس گفتید که اگر شرط مرزی یکیش برای یو و دیگری برای یو ایکس باشه دوره تناوب 4 پی هستش خب الان مشکلم با اون منفی یک دومی هست که نمی دونم با چه مقداری از دوره تناوب جمع شده که شده مثبت یه دوم در تابع جی استار البته ؟ دوره تناوب 4 باشه پس باید با 4 جمع و تفریق بشه که از حدود بازه مسئله بیشتر یا کمتر میشه.
(باز داخل متن فرمودید که ایکس بعلاوه و منهای دوره تناوب بشه)
۲- در مورد سوال دومم هم اینکه ما وقتی میگیم گسترش زوج مثلا حدود تابع در صورت مسئله بین صفر و یک هست بازه اصلی ما گیترش یافته هست یا نه بازه صورت مسئله ما هست؟
- آرش
سلام . نمودار تابع نسبت به مبدا نه زوج است نه فرد ! پس از کجا تشخیص دادید که ak ها زوج هستند ؟
- آرش
سوال 16 صفحه 432 !
با توجه به اینکه ضریب a0 در رابطه پارسوال در کتاب شما به صروت 2ao^2 و در سایر کتابها مثل کتاب آقای محمود کریمی به صورت a0^2/2 مطرح شده و در این سوال فرم اینکه مقدار a0 از a0/2 بدست آمده یا a0 مشخص نیست از کجا بفهمیم کدوم فرم رو توی فرمول پارسوال استفاده کنیم ! ؟
- آرش
- حميد
استاد x=pi مگه نقطه ی ناپیوسته برای تابع نیست پس با دیریکله f(pi)=coshpi میشود که در نهایت به همان جواب حل شده ی کتاب مرسیم.
این روش حل اشتباه است؟چرا؟
- حميد
استاد اگر بخاهیم بسط کسینوسی f(x)=sinx برای بازه ی x بین 0 و π را بنویسیم با رسم شکل تابع دوره تناوب اصلی T=π است اما اگر از فرمول استفاده کنیم T=2π است
سوال من اینه که کدوم دوره تناوب درست است؟
یا اصلا در حالت کلی تفاوتی نمیکند؟
- آرش
سلام ببخشید که من انقد سوال میپرسم :دی
توی این وسال بخش ناهمگن معادله برحسب مقادیر ثابت داده شده ولی شما تغییر متغیر رو برحسب x گرفتین ! حالا سوال من اینجاس اگه نه جمله ای برحسب x تو معادله ناهمگن بود و نه t مثل این سوال چیکار کنیم ؟
- آرش
مثال 8 صفحه 623 بعد از همگن کردن شرایط مرزی حلش خیلی سنگین و زمانبره نمیشه این بخشو ( بعد از همگن سازی شرایط مرزی) از روش مثال 7 بریم ؟
- آرش
توی مثال 1 w رو تابع x گرفتین ! از کجا بفهمیم باید w رو تابع x بکیریم یا t و یا هردو ؟
- حميد
استاد در جواب تست به این اشاره شده که چون f زوج است از cos استفاده میکنیم. دلیلش چیست؟
این نکته کجای کتاب اومده؟
- آرش
- آرش
- آرش
یه مشکل دیگهم دارم فرمولهای جمع به ضرب مثلثاتی رو از دبیرستان فراموش میکنم امکانش هست رفرنسی یا را حلی ارائه بدین که اثباتشو یاد بکیرم نه فرمولو ؟ با تشکر
به این فرمولها توجه کنید:
شماره یک [(sinαcosβ=1/2[sin(α β) sin (α-β
شماره دو [( cosαcosβ=1/2[cos(α-β) cos (α β
شماره سه [(sinαsinβ=1/2[cos(α-β)-cos (α β
توجه کنید برای اینکه نخواهید علامت منفی را نیز در سمت راست اشتباه قرار دهید،همیشه در سمت راست cos α-β را بنویسید که بدانید منفی پشتcos α-β قرار می گیرد.این سه فرمول بیشتر به کار می رود تا تبدیل جمع به ضرب،در واقع تمرکز شما بیشتر بر روی تبدیل ضرب به جمع باشد.موفق باشید
- معصومه سادات بنی جمالی
صفحه 201 ریاضی مهندسی سوال 13 راجع به تکیناش و اینکه چرا جواب صفر شده ممنون
- آرش
بخاطر سپردن فرمولهای صفحه 566 تقریبا غیر ممکنه ! شما چه روشی رو پیشنهاد میکنید؟ من نمیدونم این معادلات از کجا اومده ! نمونش توی بخش پواسون و لاپلاسم هست !
- آرش
توی بخش معادلات دالامبر ممکنه سوالی بدن که شرایط مرزی در یک سر L مثلا در x=0 گسترش فرد داشته باشه و در x=l گسترش زوج ؟ در اینصورت تکلیف معادلات و بدست اوردن مقادیر خارج از دوره تناوب چی میشه ؟ فکنم تو این حالت استفاده از حل اصلی راحتتر باشه
- آرش
ببخشید طولانی شد با تشکر.
- سهراب
استاد من منحنی مشخصه های دیود و ...فصل دوازده رو از کتاب شما برا الکترونیک هم خوندم... از ما که گذشت ولی تحلیل خازن رو هم تو کتابتون بگنجونید...کلا کتابتون جا برا هیچ سوالی نذاشته...
(البته بر خازن تو فصل دو، چون هدف یه چیز دیگه س متوجه نشدم)
- آرش
- آرش
- آرش
- mohamad
- سید
سلام استاد، سواد 16 صفحه 195:
به نظر می رسد انتگرال قابل حل است و بنده حل کردم به مقدار گزینه 1 برای حاصل انتگرال رسیدم.
روش حل اینکه z را R×e^iteta قرار دادم و انتگرال را حل کردم، قسمت مربوط به lnR بر روی تتا بین صفر و 2pi صفرشد و فقط قسمت مربوط به تتا باقی ماند که با انتگرال جز به جز به مقدار 2pi/R رسیدم که مطابق با گزینه 1 است و گزینه 4 با اینکه یک حد بالای جالب برای اندازه انتگرال است اما کوچکترین مقدار M را نمی دهد و کوچکترین حد بالا در گزینه 1 قرار دارد.
با تشکر
- yalda
- حميد
استاد تو این سوالات وقتی که میخاهیم مشتق اول y و مشتق دوم y رو بدست بیاریم حدود سیگما از 0 به 1 و 2 تغییر میکنند اما
در کتاب مدرسان حدود بدون تغییر هستند(صفر میمانند)
حالا کدوم یکی از اینها درست هسنتد؟ پاسخ نامه یا کتاب؟
- آرش
در ضفحه 432 سوال 13 توی صورت سوال ذکز شده نمایش تابع در یک دوره تناوب یعنی T=2p فرض کرده و L=P ولی شما L=2P در نظر کرفتید! چرا ؟
راستی توی بعضی سوالات فرم a0 یا a0/2 مشخص نشده و مقدار داده شده مثل سوال 10 همین صفحه. در اینصورت برای استفاده از رابطه پارسوال از کجا بفهمیم باید 2a0^2 رو حساب کنیم یا a0^2/2 ؟؟؟
- سعید انصاری
2- در مثال 66 همین فصل، چرا اگر در ناحیه d،ایکس یا ایگرگ تغییر علامت میداد نگاشت یک به یک نبود.
ممنون.
- سعیده
- سید
سلام استاد، در حل دالامبر موج صفحه 546، در تعریف G ، یک تقسیم بر c وجود دارد بنابراین پشت پرانتز یک دوم هست نه یک تقسیم بر 2c ؛ اما در صفحه 551 ، خط دوم ، قبل از G ، یک تقسیم بر 2c آمده نه یک دوم، دلیل این تفاوت چیست و از کدام فرمول باید استفاده کرد؟
با تشکر
- محمد جواد
لطفا توضیح دهید
با تشکر
Mje
- حميد
- حميد
تو یه نکته گفتید که اگر اگر (f(x زوج باشد پس ضریب انتگرال (xf(x میشود منفی مشتق (A(w و ...
1. اگه f فرد هم باشد همین شرایط برای (B(w صادق است؟
2. در کل اگر f نه زوج باشد و نه فرد آیا برای ضرایب انگرال فوریه f چنین شرایطی برقرار است؟
- حميد
در این مثال محدوده انتگرال گیری برای (A(w از 0 تا ∞ در نظر کرفته شده به جای این که از ∞- تا ∞+ در نظر گرفته شود، دلیل آن wورت سوال است که x>0
است؟ یعنی اگه x>0 در نظر گرفته نمیشد نمیتونستیم از تبدیل لاپلاس استفاده کنیم؟
- آرش
- fatemeh
- سید
سلام استاد، در صفحه 325، نکته 4، حالت دوم و همچنین صفحه 328، نکته 5، مسیر انتگرالگیری در صفحه مختلط را چگونه در نظر گرفته اید که به فرمول های مربوطه رسیده اید؟
با تشکر
- امیرحسین مختاری
انتگرال از 0 تا 2pi تابع کسری( 1 به روی (costeta+2) ) رو وقتی از ابتدا نگاه کنیم با توجه به تام بودن cos و این که در این مثال نمیتونه مخرج رو صفر کنه، ذهن رو میبره به این سمت که این یک تابع تحلیلی است و باید به روش پارامتری یا عادی حل شود، اما در ادامه و با تغییر متغیر e^teta به z متوجه می شویم که مخرج دارای دو ریشه هست که یکی در محدوده c است و با انتگرال کوشی حل می کنیم. سوال این جاست که آیا این تابع تحلیلی است یا نه؟ اگر هست چرا با یک تغییر متغیر شرایط تغییر می کند؟
لینک صورت سوال: http://uupload.ir/files/zq9e_mesal.jpg
- علیرضا
- حميد
استاد در این تست چون میبینیم نقاط تکین Lnz جز ناحیه مورد نظر نیست پس Lnz مانده ندارد.
سوال1- اگر Lnz یک نقطه تکین در این ناحیه داشته باشد چطور آن را باید پیدا کنیم؟
2-آیا اصلا ممکن است lnz مانده ای داشته باشد؟
3-در تحلیل سوال فرموده اید که چون در گزینه ها عدد داریم پس نیاز به چک کردن تحلیلی بودن lnz نیست. دلیل این چیست؟
- علیرضا
- محمودرضا صدیق
- مجتبی 6816
مثال 50 صفحه 222 اصلا متوجه نمیشم چرا تابه داخل انتگرال از توان 3 به توان 5 تبدیل شده؟؟؟؟؟؟
از بابت مثال های جدید و دشوار کتابتان سپاسگذارم
- حميد
استاد چندتا سوال داشتم
1.چرا برای تکین برداشتنی بسط لوران دارای توان های منفی نیست؟
2.برای تکین تنها، بسط تابع فقط شامل توان های منفی است یا شامل توان های متبت هم میشود؟
3.تفاوت تکین تنها و تکین اساسی چیست؟
- کسری
- راضیه یاراحمدی
مثال9صفحه172 قسمتI3 جاییک 2pوp/2را جایگذاری میکنیم درt چطور e^2i2pمیشود- 1p(i
- احمد
سوالات ریاضی مهندسی و معادلات آزمون مرحله اول بیش از حد پیچیده بود، جوری که من همه سوالات مثلا معادلات رو میومدم تا سر مرز جواب بین دو گزینه گیر میکردم
بنظر من نیاز به این همه پیچ و خم تو سوالات نبود
سوالات کنکور هم اینقدر گیج کننده نیستن
مثلا شما سوالات رو برای کسانی آوردین که صد درصد مطالب رو فول بودن و هیچ ارزشی برای مثلا پنجاه درصدها و یا هفتاددرصد مسلط ها قایل نشده بودین، عین طراحان محترم سوالات کنترل خطی کنکور سراسری
بنظر من که غیر استاندارد بودن سوالات ، در صورتی که تو آزمون های خود سنجی مرحله اول و دوم اینجور نیورده بودین و این یعنی غافل گیری محض
- کسری
- حميد
استاد از معادله لاپلاسی که مشتق بر حسب z و zبار هست میشه برای تحلیلی نبودن تابع (f(zای که برحسب z هست استفاده کنیم؟ یعنی از f یبار برحسب z و یبار برحسب zبار مشتق بگیریم اگر مساوی صفر مشد بگیم تحلیلی نیست.
- راضیه یاراحمدی
مبحث نگاشت مثال 8صفحه99 یامثال11صفحه 100راه حلشون چطوره هرچی میخونم متوجه نمیشم کلا درمورد مثالهایی ک تصویری تحت یک نگاشت میخان رو توضیح میدین توروخدا راهنمایی کنین ازتوضیحات قبلیتون بینهایت ممنونم
- mohamad
استاد خودش توی جواب گفته نقطه ی ویژه اساسی است ولی در گزینه ها قطب رو علامت زده خب باید گزینه دو نه صفر نه قطب درست باشه دیگه لطفا راهنمایی کنید
- راضیه یاراحمدی
ببخشید مبحث نگاشتوهرچی میخونم متوجه نمیشم میشه یه توضیح بدین درمورد نگاشت هاییک معرفی کردین خیلی سخته
- راضیه یاراحمدی
ریاضی مهندسی صفحه 89اینک گفتین نقطه گذاری وعددگذاری کنیم توتست ها انتخاب این عدد ها چطوری؟دلخواه یاباید ازقانون خاصی پیروی کنه لطف کنین راهنمایی کنین
- RealFlow
لطفا حل کنید برام اون جواب که نوشتید تشکر میکنم ازتون ولی باز متوجه نشدم لطفا کمکم کنید با حل کردنش iچطور نوشته شد مقادیر2 و 3 و+- چطور اومده خلاصش کنید برام
- راضیه یاراحمدی
- راضیه یاراحمدی
ببخشید استاد معادلات دیفرانسیل صفحه 54مبحث پوش دسته منحنی در آخر وقتی بجای cبتوان 2جایگذاری میکنیم مثلا. y=cx+1/c
c^2=1/x. وقتی درمعادله اول همه رو بتوان دو میرسانیم آخرش +2xمینویسیم از کجاآمده؟
- RealFlow
چطور z شده برابر e شده 2k پی.ای به رویn
چطور ربدست امده راانماییم کنیید
------------------------------------------------------
مثال 40
اینجانیز مثل مثال بالا چطور شده z برابر e با 2kپی 0 به روی 6
میدانم چرا بروی 6 هست منظورم صورت کسرش چطور میشه این که نوشتین مشکل اصلی من تواینجور مساله ها چطور مقدار e نوشتن
تو مثال 41و42 هم همینطور چطور مشکلم رو حل کنم مقادیر e رو بدست بیاریم
- RealFlow
- راضیه یاراحمدی
معادلات دیفرانسیل صفحه 55 مبحث معادلات لاگرانژ قسمت آخرش معادلهy=xp بتوان 2 منهای پی بتوان سه چطور تشکیل شده؟لطف کنین توضیح بدین همشوفهمیدم جز این یک قسمتش باتشکر
- احمد
این تابع در تمام صفحه تحلیلیه طبق شرایط کوشی ریمان در حالی که شما گفتین در ربع اول و سوم
چرا؟
- کاوه
چرا در بسط فوریه ی سینوسی y=sinx ،وقتی xبین صفر و پی میباشد ، ضریب bn صفر میشود، همچنین در بسط کسینوسی ، y=cosx وقتی x بین صفر و پی هستش ،نیز ضریب an صفر میشود ، علتش چیه؟
- احمد
ناحیه محصور بین دودایره رو از رو فرمول خاصی باید بدست آورد، یا تجربه و تمرین
الان من نمیدونم چجور شما به زد مساوی یک سوم بعلاوه یک سوم آی رسیدن
- سینا
- Mehdi
در حل این تست چرا اندازه e^pi/3 -1 را برابر یک گرفته اید در صورتی که باید برابر جزر 3 باشد
با تشکر
- kambiz
- حميد
استاد برای یدست آوردن سری فوریه (f(x)=sinx ; 0>x<π) آیا میتوان T=2pi در نظر گرفت یا حتما باید کوچکترین دوره تناوب یعنی T=pi در نظر گرفته شود؟
- پیام آراسته
سپاس از پاسخ های باحوصله تون.
استاد توی ابتدای درسنامه 2 از فصل 4 که انواع نقاط تکین رو تعریف کردید، فکر نمی کنید که تعریف نقطه تکین و نقطه تکین تنها جابه جا شده؟
- حميد
استاد اگر تابعی داشته باشیم مثل تابع زیر و بخواهیم سری فوریه و بسط های نیم دامنه ای سینوسی و کسینوسی آن را پیدا کنیم، سری فوریه و این بسط ها چه رابطه ای با هم دارند؟
آیا در سری فوریه این تابع باید T=2l=2pi در نظر گرفته شود?
(f(x)=1 ; 0>x<π و f(x)=0 ; π>x<2π)
- RealFlow
ممنون ازاینکه سوالات قبلیم جواب دادید واقعا خوشحالم ازاینکه باشماهستم خدا همیشه یاورتان باشد
- RealFlow
- RealFlow
z* منظور z بار است.
- سید
در بالای صفحه 114 و با عنوان "توجه" فرمودید که یک راه ساده تر هست که ما را به ربع اول می رساند؛ بنده راهی را که فرمودید امتحان کردم و به ربع دایره در ربع اول رسیدم نه کل ربع اول. ممنون میشوم توضیح فرمایید.
- احمد
در جواب تست 19صفحه 560
خودتون گفتین بازه تغیرات ایکس بین صفر و یک هستش ولی ایکس رو درآوردین منفی ال چهارم
منفی ال چهارم که تو بازه صفر و یک نیست مهندس
دقیقا بالای جایی که نوشتین جمع صفر است
- سهراب
اگه مقدوره میشه مطلب گسترش زوج و فرد رو بیشتر باز کنید؟
- پورنگ
در فصل اول کتابتون گفتید که برای مشتق گیری باید فقط از ریمان استفاده کنیم..فقط در یکی از مثال های (مثال 46 چاپ 18) نتیجه گرفتید مشتق چند جمله مختلط مثل مشتق گیری حقیقی مختلطه...
سوال من این هست که چرا مثلا در فصل های دیگر مثلا فصل سوم بدون این که از ریمان استقاده کنیم از توابعی مثل exp یا cosh و.... همانند توابع حقیقی مشتق میگیرم...؟(یعنی از همون فرمول های آماده مشتق گیری توابع حقیقی معروف).آیا قضیه ای یا نکته ای در این مورد وجود دارد ؟
- علیرضا
- محمد
- mohamad
و تشکر فراوان از پاسختون به سوالم در مورد قضیه گاوس
دلسوزی و توجهتون کمک بزرگی برای ما هست
استاد من چند مورد اشکال تو سوالات ریاضی چاپ قدیم داشتم که تو چاپ جدید حذف شدند فکر کنم صورت سوالشون ایراد داشته که حذف کردید درسته ؟ پس لزومی نداره پیگیر بشم ؟
و در سری های مختلط در سوال 37 صفحه 226 در جواب گفته سری "همگراست با توجه به قوانین p سری ها " این قوانین را از کجا می شود یاد گرفت مثلا (n^(-1/2 واگراست و n^-3 همگراست
سری های به فرم 1 تقسیم بر n^p با شرط p بزرگتر از 1 ،همگراست و با شرط p کوچکتر یا مساوی 1 واگرا هستند. این مسایل مربوط به ریاضی 1 است اما در همین حد برای ریاضی مهندسی کفایت میکند.سوالاتی که گفتید حذف شده اند، به دلیل اینکه مربوط به رشته ریاضی و محض بودند (توابع مختلط)در چاپ جدید دیگر لزومی به مطرح شدن نداشت..ضمن اینکه حتما چاپ بیستم ریاضی مهندسی را مطالعه کنید.موفق باشید
- احسان
برای برقراری قضیه گرین باید f روی ناحیه D و مرز C تحلیلی باشد؟
بله،اگر f مختلط است(ریاضی مهندسی)باید بگوییم روی D و مرز C تحلیلی باشد.
اگر f تابع حقیقی است(ریاضی عمومی)باید f روی D و C مشتق پذیر باشد.
- احسان
صفحه 110 چاپ جدید مثال 30 اگر قرار دهیم:
cosh z=cos iz=sin(iz +pi/2 و اینگونه نگاشت را انجام دهیم نا حیه مرد نظر فقط به ربع اول نگاشت میشود برخلاف روش کتاب که به ربع اول و دوم نگاشت میشود. یعنی از دو راه مختلف به دو ناحیه مختلف.چرا اینجوری میشه؟
ممنون میشم راهنمایی کنین

- mohamad
تو خود سوال و پاسخش هیچ اشکالی ندارم اما گزینه های 3 و 4 رو نمیفهمم گه چطور میشه رد کرد؟ و اصلا منظورش چیه نگاشت یک به یک چیه

- mohamad
جواب این سوال در شکل صفحه ی 82 باید می شد قسمت محصور بین دو سهمی تو در تو چرا شده نیم دایره ؟ فرمولی هم که بدست آورده مربوط به سهمی است ؟
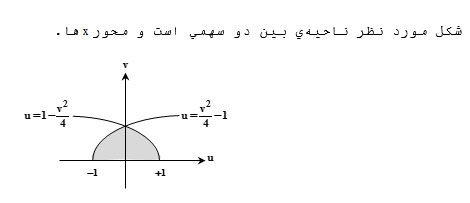
ممنون از لطفتون..فقط با توجه به شماره صفحه و سوالی که مطرح کردید متوجه شدم که کتاب چاپ قدیم رو دارید مطالعه می کنید،در صورت امکان حتماچاپ بیستم رو تهیه کنید،چونکتاب چاپ جدید تفاوت های بسیاری کرده است.هم از نظر درسنامه و هم از نظر سوالات تالیفی.
- سعید انصاری
در صورت وقت داشتن تمام رشته ها را حل کنید.اما اگر با کمبود وقت مواجه هستید کنکور های برق،مکانیک و کامپیوتر را حل کنید.
اما همیشه در اولویت کارتان تستهای تالیفی باشد.
موفق باشید
- سعید انصاری
میشه سوال 117 تست های طبقه بندی شده فصل اول(مجموعه ریاضی-87)رو بدید.
تشکر
- حسین رضایی
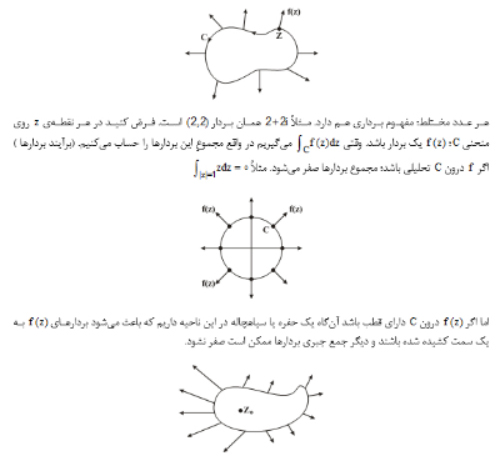
آیا میتوان درک هندسی از انتگرال گیری مختلط مثلا روی یک خم بسته داشت. که معنای پاسخ انتگرال چیه؟ یا مفهوم هندسی مانده. و مسائل مشابه
با تشکر
- محمد حسن کسایی
بنده کتاب "حل سوالات ریاضی مهندسی" شما را مطالعه کرده ام وسوالم در مورد تست شماره 50 رشته مکانیک است. مگر اینگونه نیست که در جواب این تست باید مقدار کمان sin، مقدار جذر توان e باشد، در گزینه 2 که شما به عنوان جوابی معرفی کرده اید طبق دستورالعمل شما باید عدد 3 هم در کمان sin باشد که اینطور نیست ودر گزینه 4 این دستورالعمل رعایت شده است (صرف نظر از. مقدار c2) استدلال شما چیست؟
با تشکر
- حسین رضایی
صفحه 136 ، مورد هشتم بسط تیلور ، نباید شرط |z|<1 را داشته باشد؟
- پوریا تورکش
- محمد رضا م















