ریاضی عمومی 1(میکروطبقه بندی شده)
برخی رشته ها این کتاب با نگارش ساده و اجتناب از بیان مطالب غیرضروری سعی داشته داوطلبان آزمون کارشناسی ارشد در کمترین زمان بدون نیاز به کتب دیگر بهترین نتیجه گیری را داشته باشند.
مشاهده توضیحات کامل شابک: 9789641125815
تعداد صفحات: 672
نوبت چاپ: 23
تاریخ چاپ: 1398
مولف : مهندس حسین نامی
برای دانلود رایگان کتاب ریاضی عمومی 1(میکروطبقه بندی شده) مدرسان شریف (بخشی از کتاب) برروی لینک زیر کلیک نمایید. دانلود قسمتی از کتاب نوع فایل: pdf
حجم فایل: 1MB

بسياري از مطالب درس رياضي عمومي (۱)، قبل از ورود به دانشگاه آموزش داده ميشوند. اما غير از مباحثي نظير تابع، حد و تاحدودي مشتق، ساير مباحث در رياضي عمومي (۱) بعد از ورود به دانشگاه بسيار پيشرفتهتر مورد بررسي قرار ميگيرند؛ البته فصولي مانند «اعداد مختلط» و «مختصات قطبي» از جمله مباحثي هستند كه صرفاً پس از ورود به دانشگاه آموزش داده ميشوند. اين آشنايي قبلي، مزايايي دارد كه مهمترين آن، بالا رفتن سرعت يادگيري است از طرفي در صورت غفلت از خواندن دقيق و مرور مسائل متنوع ممكن است تهديدي براي داوطلب باشد. در واقع بسيار ديده شده است كه داوطلبان با اعتماد به نفس ناشي از دوره قبل از دانشگاه از مطالب اين درس سطحي عبور ميكنند و اتفاقاً در آزمونها، ناتواني آنها در پاسخگويي به سؤالات رياضي عمومي (۱) از رياضي عمومي (۲) بيشتر است!! البته اين موضوع ميتواند به علت بالا بودن قابليت طرح سؤالات متنوع در مباحث اين درس (نسبت به رياضي عمومي ۲) نيز باشد. به همين دليل در اين كتاب سعي شده است كه مطالب از پايه تا پيشرفته و با در نظر گرفتن اينكه داوطلب هيچ سابقه مطالعاتي در اين درس ندارد، با توضيحات فراوان فارسي آموزش داده شود و اطمينان دارم كه صرفاً با خواندن و دوره كردن اين كتاب ميتوانيد تسلط كافي در اين درس را براي هر آزموني پيدا كنيد و به هيچ كتاب ديگري نيز نياز نداشته باشيد.
از ويژگيهاي بارز اين كتاب كه آن را از ديگر كتابهاي موجود در اين زمينه متمايز ميكند و به گواه رتبههاي تكرقمي ساليان گذشته و اساتيد مطرح در اين درس، يكي از متفاوتترين و بينظيرترين كتابهاي موجود در اين زمينه ميباشد، موارد زير را ميتوان نام برد:
۱) نگارش سادهي اين كتاب و استفاده از فارسينويسي در كنار مطالب و فرمولهاي رياضي و همچنين اجتناب از اثبات فرمولهاي پيچيده رياضي و مطالب غيرضروري كه باعث ميشود خواننده بسيار راحت با كتاب ارتباط برقرار كرده و به اصطلاح با رياضي آشتي كند!
۲) هر فصل كتاب بهصورت ميكروطبقهبندي تنظيم شده است. به اين مفهوم كه هر فصل به زيربخشهايي تحت عنوان «درسنامه» تقسيم شده و پس از آموزش و توضيحات كامل، مثالهای تألیفی و تستهای منتخب آزمونهای کارشناسی ارشد سالیان گذشته
(با تأکید بر چند سال اخیر) آورده شده است. اين روش ذهن را بسيار منظم كرده و اشتياق يادگيري را بالاتر ميبرد.
۳) كتاب مبتني بر حل مسأله و ارائه تستهاي متنوع و جالب جهت ايجاد تبحر در حل سؤال است و بياغراق ميتوان گفت كمتر سؤالي ممكن است در آزمونهاي آينده طرح شود كه عين يا شبيه آن در اين كتاب نباشد! ضمن اينكه از حيث تعداد مثالهاي متنوع حل شده نيز ميتوان كتاب را در بين كتب حال حاضر بينظير دانست.
۴) برخلاف ديگر كتابها كه سؤالات تكراري كنكورهاي سالهاي قبل به خصوص آزمونهاي ۱۰ تا ۱۵ سال گذشته را به عنوان مثال آموزشي متن كتاب آوردهاند! در اين كتاب سؤالات مختلف (تألیفی و کنکورهای سالیان اخیر) به صورت هدفمند و متنوع و از سطح ساده به سخت بهگونهاي طراحي شدهاند كه هر خوانندهاي به فراخور وضعيت علمي خود بهره كامل را از آن ببرد؛ چرا كه عقيده بنده بر اين است كه داوطلبان بايد در اين درس آنقدر مثالهاي متنوع و البته غيرتكراري ببينند كه در مدت زمان كم در روز آزمون، به سرعت شروع به حل سؤالات كنند و هيچ سؤالي برايشان ناآشنا نباشد.
۵) برای داوطلبانی که نیاز به تمرین بیشتر دارند، سؤالات و پاسخهای تشریحی اضافی (چه سؤالات تألیفی و چه سؤالات کنکور سالیان گذشته) بر روی سایت www.h-nami.ir قرار داده شده است که میتوانند به صورت رایگان آن را دانلود نمایند.
۶) سؤالات رياضي عمومي (۱) و (۲) رشتههايي كه بيشترين شركتكننده را دارند (عمران، MBA، مكانيك، رياضي و آمار و کامپیوتر) سال ۱۳۹۸ در انتهاي كتاب رياضي عمومي (۲) آورده شده است. لازم بهذكر است بهدليل قرار گرفتن سؤالات رياضي عمومي (۱) و (۲) در كنار هم، اين بخش ميتواند محك خوبي براي داوطلبان در روزهای پاياني نزديك به آزمون اصلي باشد. اصولاً پيشنهاد بنده اين است كه در هفته آخر قبل از آزمون اصلي اين سؤالات و پاسخها مطالعه شوند و ترجيحاً داوطلبان مانند آزمون اصلي و در همان زمانبندي به اين سؤالات پاسخ دهند تا نوعي خودسنجي نيز صورت گرفته باشد. لازم است اشاره كنم سؤالات و پاسخهاي تشريحي آزمونهاي كارشناسي ارشد ساير رشتهها بر روي وب سايت www.h-nami.ir قرار گرفته است و داوطلبان ميتوانند در صورت نياز آنها را دانلود (رايگان) كرده و مطالعه كنند.
۶) مطالب اين كتاب به گونهاي تنظيم شده كه ميتواند به عنوان مرجع كامل درس «رياضي عمومي (۱)» جهت موفقيت در امتحانات پايان ترم دانشگاهي نيز مورد استفاده قرار بگيرد. برخی از مسائل مهم پايان ترم دانشگاههاي جهان و ايران در اين كتاب ارائه و به آنها پاسخ تشريحي داده شده است.
با توجه به اينكه هيچ تأليفي خالي از اشكال نيست، لذا از همه استادان و دانشجويان تقاضا دارم، اشكالات اين كتاب را از طريق وب سایت شخصی اینجانب به آدرس www.h-nami.ir اطلاع دهند در ضمن در این وب سایت پشتیبانی و رفع اشکال درسی نیز صورت میگیرد.
فصل اول: تابع
درسنامه1: انواع تابع و مفاهيم مرتبط با آن ......................... 1
مفهوم تابع ............................................... 1
اعمال جبري روي توابع ..................................... 2
انواع تابع ............................................... 2
خواص قدرمطلق ............................................. 3
بررسي تقارنهاي يك منحني .................................. 5
توابع زوج يا فرد ......................................... 7
نكات مهم در مورد توابع زوج و فرد ......................... 8
توابع يك به يك ........................................... 8
تابع پوششي (پوشا) ........................................ 9
درسنامه2: توابع معکوس و ترکیب توابع ............................ 11
توابع معكوس ............................................. 11
نحوه بهدست آوردن تابع معكوس ............................. 11
تركيب دو تابع ........................................... 14
بهدست آوردن g(x) .......................................... 16
بهدست آوردن ضابطهي.................................... 16
درسنامه3: توابع مثلثاتی و متناوب و وارون مثلثاتی ................. 18
توابع مثلثاتي ........................................... 18
توابع متناوب ............................................ 20
توابع وارون مثلثاتي ..................................... 23
روابط و خواص مهم توابع وارون مثلثاتي .................... 24
درسنامه4: توابع هیپربولیک و وارون هیپربولیک ..................... 26
توابع هيپربوليك ......................................... 26
معكوس توابع هيپربوليك ................................... 28
روابط بين نسبتهاي مثلثاتي و توابع هيپربوليك ............. 29
درسنامه 5: بهدست آوردن دامنه و برد توابع ........................ 30
محاسبه دامنه توابع ...................................... 30
نامساويهاي لگاريتمي ..................................... 31
دامنه توابع وارون ....................................... 33
برد تابع ................................................ 33
تعيين برد توابع شامل جزء صحيح.................... 37
برد توابع نمايي و لگاريتمي .............................. 38
تساوی دو تابع ........................................... 40
درسنامه 6: مفهوم فاكتوريل و بسط دوجملهاي ........................ 41
فاكتوريل ................................................ 41
بسط دوجملهاي نيوتن ...................................... 42
درسنامه 7: مقاطع مخروطي (منحنيهاي درجه دو) ...................... 44
فصل دوم: حد و پيوستگي
درسنامه1: تعاریف حد، محاسبهی مستقیم حد، حدود چپ و راست ........ 47
تعریف حدود چپ و راست ................................ 47
ويژگي جايگذاري مستقيم در ضابطهي تابع ................ 47
قواعد و قضایای حد ................................... 47
تعريف صفر حدي ( و)، ، ، و صفر مطلق ........ 48
در چه نوع حدودي حتماً لازم است هم حد چپ و هم حد راست را حساب كنيم؟ 51
موقعیت حدی نقطه ..................................... 56
درسنامه 2: حالت مبهم ................................. 58
رفع ابهام از حالت مبهم............................. 58
درسنامه 3: حالت مبهم ................................ 72
درسنامه4: حالت مبهم ................................. 79
درسنامه5: حالت مبهم ................................ 83
درسنامه6: حالت مبهم ................................... 87
درسنامه7: حالت مبهم .................................. 88
درسنامه8: حالت مبهم ................................... 89
درسنامه 9: پيوستگي تابع ................................ 94
جهش انفصال تابع ..................................... 97
چند نكته در مورد توابع پيوسته ....................... 97
پيوستگي تابع در يك فاصله ............................ 98
تعريف ناپيوستگي رفع شدني و رفع نشدني ................ 99
بهدست آوردن نقاط انفصال توابعي به فرم ..... 100
درسنامه10: قضیه مقدار میانی (بولتزانو) .................... 102
درسنامه 11: مجانب ................................... 104
روشهای تعیین مجانب مایل ............................ 106
مجانب توابع پارامتري ............................... 110
مجانب توابع ضمني ................................... 111
فصل سوم: مشتق و كاربرد مشتق
درسنامه1: مفهوم مشتق و فرمولهاي مشتقگيري .................. 112
تعبیر هندسی و تعریف مشتق............................ 112
مشتق چپ و راست ..................................... 113
رابطهی بين مشتق و پيوستگي........................... 114
نقاط مشتقناپذیر توابع............................... 116
قواعد مشتقگيري...................................... 118
نوشتن تابع مشتق توابع چند ضابطهاي .................. 119
مشتق حاصلجمع، حاصلضرب و تقسيم دو عبارت.............. 120
استفاده از لگاريتم در مشتقگيري...................... 121
مشتقات مراتب بالاتر................................. 123
محاسبهی مشتق مرتبه ام............................. 124
فرمول لایبنیتز ...................................... 127
بررسی مشتقپذیری سه تابع مهم ........................ 128
مشتق منحنیهای پارامتری ............................. 133
عامل صفركننده در مشتق .............................. 134
نرخ تغييرات ........................................ 134
چند نكته تكميلي در مورد مشتق........................ 135
درسنامه2: مشتقگیری ضمنی ..................................... 136
درسنامه3: قاعده زنجیرهای مشتق ................................ 140
مشتق تابع.......................................... 140
درسنامه4: مشتق تابع معکوس .................................... 143
درسنامه5: استفاده از تعریف مشتق در حل مسائل ..................... 146
چه زمانی لازم است از تعریف مشتق استفاده کنیم؟............ 146
بررسي توابعي به فرم كلي و ( و ) 149
درسنامه6: آهنگ تغيير ....................................... 155
آهنگ متوسط و آهنگ لحظهاي تغيير.......................... 155
آهنگ تغيير در فيزيك..................................... 155
آهنگ تغيير در اقتصاد.................................... 155
آهنگ تغيير در زيستشناسي................................. 156
كميتهاي داراي رشد (يا زوال) نمايي....................... 156
نيمهعمر مواد راديواكتيو................................. 157
آهنگهاي وابسته.......................................... 158
دستورالعملِ حلِ مسائل آهنگهاي وابسته...................... 158
درسنامه7: خطوط قائم و مماس بر یک منحنی ........................ 166
معادله خط مماس و قائم بر يك منحني ...................... 166
تحت مماس و تحت قائم .................................... 170
طول مماس و طول قائم..................................... 171
منحنيهاي مماس برهم...................................... 171
زاويه بين دو منحني...................................... 174
زاويه بين دو نیممماس.................................... 175
يافتن معادله خط مماس يا قائم از نقطهاي خارج منحني ...... 176
درسنامه8: نقاط اکسترمم، عطف و تشخیص رفتار تابع ................... 178
تعريف ماكزيمم و مينيمم نسبي (موضعي)..................... 178
تعريف ماكزيمم و مينيمم مطلق............................. 178
نحوه تعيين نقاط ماكزيمم و مينيمم نسبي................... 179
تعيين نقاط Max و Min مطلق تابع.......................... 184
بررسي وجود Max و Min مطلق روي بازهي باز............. 186
استفاده از آزمون مشتق دوم چه زماني مناسب است؟........... 188
چند نكته در مورد نقاط اكسترمم توابع..................... 190
چند نكته در مورد ارتباط نقاط بازگشت و اكسترممهاي نسبي... 191
پيدا كردن برد توابع با استفاده از مشتق.................. 192
تعيين صعودي و نزولي بودن تابع به كمك مشتق............... 193
رابطهي بين مفاهيم صعودي و نزولي، يك به يك بودن و يكنوا بودن 196
بررسي چند تابع مهم...................................... 197
تعريف تقعر.............................................. 198
تعريف نقطه عطف و روشهاي بهدست آوردن آن.................. 199
روش بهدست آوردن نقطه عطف................................ 200
آزمون مشتق سوم در تعيين نقطه عطف........................ 204
استفاده از بسط تيلور براي تشخيص نمودار حول يك نقطه... 205
روشي ديگر در تعيين نقاط عطف، ماكزيمم و مينيمم نسبي...... 206
روابط بين نمودارهاي، و............................. 207
درسنامه9: مسائل بهينهسازي .............................. 213
دستورالعمل حل مسائل بهينهسازي....................... 216
مسائل بهينهسازي در اقتصاد........................... 231
چند نكته براي محاسبهي مقادير اكسترمم مطلق بدون استفاده از مشتق 232
درسنامه10: قضاياي مقدار ميانگين، رُل و كشي ................. 234
كاربردهاي قضيهي مقدار ميانگين ...................... 239
قضيهي مقدار ميانگين در حالت كليتر .................. 242
درسنامه11: تعريف ديفرانسيل و محاسبه تقريبي مقدار تابع ....... 243
مفهوم ديفرانسيل تابع ........................... 243
تقريب خطي مقدار (كاربرد ديفرانسيل).............. 244
فصل چهارم: انتگرال
درسنامه1: فرمولها و تغییر متغیرهای مناسب در انتگرالگيري ...... 247
فرمولهاي مهم انتگرال................................ 247
خواص انتگرال نامعين................................. 248
انتگرال معین ....................................... 251
قضیه اساسی حساب دیفرانسیل و انتگرال ................ 252
از كجا بفهميم از چه تغيير متغيري بايد استفاده كنيم؟ 256
تغيير متغير در انتگرالهاي شامل راديكال ............. 257
انتگرال دیفرانسیل دو جملهای و قضیهی چبیشف .......... 263
استفاده از روشهای ابتکاری در محاسبهی انتگرالها ..... 266
درسنامه2: محاسبهي انتگرالهاي شامل توابع مثلثاتي یا هيپربوليك ... 269
محاسبهي انتگرالهاي sinو cos با توان فرد ............. 269
محاسبهي انتگرالهاي sinو cos با توان زوج ............. 269
محاسبهي انتگرالهاي به صورت كه در آنها m و n اعدادي صحيح هستند.......................................... 269
محاسبهي انتگرال وقتي m و n اعدادي گويا باشند. 270
محاسبهي انتگرالهايو (n عدد طبيعي است)..... 270
محاسبهي انتگرالهايي به صورت كلي....... 271
محاسبهی انتگرالهای حاصلضرب دو جمله سینوسی و کسینوسی 272
محاسبهي انتگرالهايـي بهصورت............ 273
محاسبهي انتگرالهايـي به فرم كلي........ 276
محاسبهي انتگرالهايي به صورت كلي....... 277
درسنامه3: روش انتگرالگيري جزء به جزء ..................... 278
انتگرالگيري جزء به جزء به كمك تشكيل جدول............ 289
كاهش مرتبهي انتگرالگيري و استفاده از قاعدهي جزء به جزء 293
درسنامه 4: انتگرالگیری به روش تجزیه کسرها (تجزیه کسرهای جزئی) .. 295
انتگرالگیری به روش تجزیه کسرها (تجزیه کسرهای جزئی).. 295
محاسبهی ضرایب در کسرهای جزئی........................ 296
درسنامه5: نکات و خواص مهم انتگرالهای معین ................. 301
چند فرمول دیگر از انتگرالهای معین ................... 317
قضیه مقدار میانگین در انتگرال (محاسبهی مقادیر متوسط توابع) 317
تعمیم قضیه مقدار میانگین ............................ 319
درسنامه 6: محاسبهی انتگرالهای شامل جزء صحیح و قدرمطلق ....... 320
محاسبهی انتگرالهای شامل براکت (جزء صحیح) ........... 320
محاسبهی انتگرالهای شامل قدرمطلق .................... 323
درسنامه 7: انتگرالهای غیرعادی (ناسره) ......................... 326
انتگرالهای غیرعادی (ناسره) ............................. 326
ناسرگی ترکیبی در انتگرالها ............................. 333
بررسی وضعیت همگرایی و واگرایی در انتگرالها ............. 334
استفاده از همارزی در بررسی همگرایی و واگرایی انتگرالها . 336
آزمون مقایسه............................................ 342
همگرایی مطلق و همگرایی مشروط............................ 347
چند نکته در مورد دو انتگرال مهم ........................ 347
تعریف مقدار اصلی کوشی ............................. 350
استفاده از تبدیل لاپلاس در حل برخی از انتگرالها .......... 350
انتگرالهای فرولانی ...................................... 351
درسنامه 8: مشتقگیری از انتگرال ............................... 352
اولین قضیهی اساسی حساب دیفرانسیل و انتگرال ............. 352
مشتقگیری از انتگرال .................................... 352
تعمیم فرمول مشتقگیری از انتگرال ........................ 365
انتگرالهای وابسته به پارامتر ........................... 368
درسنامه 9: معرفی توابع گاما و بتا ............................ 374
تابع گاما .............................................. 374
تابع بتا ............................................... 378
خواص مهم تابع بتا ...................................... 378
فصل پنجم : كاربرد انتگرال
درسنامه1: محاسبهي حد مجموع به كمك انتگرال معين ................ 384
سه بحث مفهومي و مهم..................................... 394
درسنامه2: محاسبهي سطح محصور ................................. 398
محاسبهي مساحت محصور بين يك منحني و محورها............... 398
محاسبهي مساحت محصور بين دو منحني........................ 405
درسنامه3: محاسبهي حجم حاصل از دوران ............................ 415
محاسبهي حجم به روش ديسك (روش قرصي)...................... 415
روش «پوسته استوانهاي» براي بهدست آوردن حجم.............. 425
نحوهي استخراج فرمولهاي حجم.............................. 432
جمعبندي و مطالبي جهت به خاطر سپردن فرمولها.............. 433
قرار گرفتن ناحيه در دو سمت محور دوران................... 433
محاسبهي حجم با استفاده از سطح مقطع...................... 433
درسنامه4: محاسبهي طول قوس منحني .............................. 437
تعريف تابع طول قوس...................................... 445
درسنامه5: محاسبهي مساحتِ سطح حاصل از دوران يك منحني ............... 446
نحوهي استخراج فرمولِ محاسبهي مساحتِ سطح حاصل از دوران..... 452
درسنامه6: محاسبهي مختصات مركز ثقل (قضیه پاپوس گلدن) .............. 453
جرم و چگالي............................................... 453
چگالي غيرثابت............................................. 453
گشتاورها و مرکز جرم ...................................... 454
جمعبندي................................................... 455
محاسبه گشتاورهاي استاتيك.................................. 456
محاسبه مختصات مركز ثقل يك ناحيه مسطح ..................... 456
مختصات مركز ثقل يك منحني مسطح ............................ 456
قضاياي گلدن ـ پاپوس....................................... 459
نحوهي استفاده از قضاياي گلدن ـ پاپوس...................... 459
فصل ششم: دنباله و سري
درسنامه1: تعريف و بررسي رفتار دنبالهها .................... 462
بررسي همگرايي و واگرايي دنبالهها.................... 463
محاسبه حدود و عدد همگرايي در دنبالهها............... 464
چند مثال متنوع دیگر ................................ 475
قضیه اشتولز ........................................ 476
بررسي وضعيت همگرايي حاصل جمع، تفريق، ضرب و تقسيم دو دنباله 478
دنبالههاي صعودي و اكيداً صعودي....................... 478
دنبالههاي نزولي و اكيداً نزولي....................... 478
روشهاي تعيين كران بالا يا كران پايين دنبالهها........ 481
درسنامه2: دنبالههاي بازگشتي ............................. 483
دنباله با رابطهي بازگشتي............ 486
درسنامه3: تعریف انواع سری و شرایط لازم برای همگرايي سريها ..... 488
نماد سيگما.......................................... 488
خواص سيگما.......................................... 488
سريهاي عددي نامتناهي ............................... 490
همگرايي يا واگرايي سريها............................ 490
بررسي وضعيت همگرايي؛ جمع، تفريق، ضرب و تقسيم دو سري. 491
درسنامه4: آزمونهای همگرایی برای سریهای مثبت ................ 492
سری هندسی و شرط همگرایی ............................ 492
استفاده از سری ................................... 492
آزمون مقایسه ....................................... 496
آزمون خارج قسمت (مقایسه حدی) ....................... 498
آزمون نسبت (آزمون دالامبر) .......................... 501
آزمون ریشهی ام (آزمون کوشی) ...................... 502
آزمون انتگرال ...................................... 505
آزمون آبل .......................................... 505
آزمون رابه ......................................... 506
آزمون تراکم کوشی ................................... 507
سریهای متناوب ...................................... 510
همگرایی مطلق و مشروط ............................... 512
درسنامه5: به دست آوردن حاصل سریهای عددی ................... 517
مقدمهای برای ورود به بحث سریهای تلسکوپی ............. 517
سریهای تلسکوپی ...................................... 518
سریهای هندسی ........................................ 527
استفاده از تصاعد هندسی در حل برخی مسائل فیزیکی و هندسی 532
نماد پای.......................................... 537
درسنامه6: تعریف سریهای توانی، محاسبهی شعاع و فاصلهی همگرایی آنها 541
سريهاي تواني ........................................ 541
محاسبه فاصله همگرايي و شعاع همگرايي سري تواني ....... 541
نكته مهم و مكمل در تعيين باز يا بسته بودن بازه همگرايي 551
سريهاي تابعي و بهدست آوردن ناحيه همگرايي آنها ....... 556
درسنامه7: سريهاي تيلور و مكلورن و کاربرد آنها ............... 562
مشتق و انتگرال گرفتن از سريهاي تواني ............... 573
به دست آوردن حاصل برخي از سريها با استفاده از سريهاي مكلورن .................................................... 578
بازي با e .......................................... 588
كاربردهاي ديگر سري تيلور ........................... 593
سريهاي دوگانه ...................................... 598
فصل هفتم: دستگاه مختصات قطبي
درسنامه1: دستگاه مختصات قطبي و مفاهيم مرتبط به آن ................ 600
تعريف دستگاه مختصات قطبي................................ 600
ارتباط بين مختصات دكارتي و قطبي......................... 601
تبديل معادلات در دستگاههاي مختصات قطبي و دكارتي.......... 602
نمايش چند منحني و ناحيه در مختصات قطبي.................. 605
خط مماس و قائم بر يك منحني قطبي......................... 605
محاسبهي زاويه بين شعاع حامل و خط مماس بر يك منحني قطبي.. 608
رسم نمودار منحنيهاي قطبي................................ 609
بررسي تقارن در منحنيهاي قطبي............................ 610
روش ديگر براي رسم منحنيهاي قطبي......................... 611
يافتن نقاط برخورد نمودارهاي قطبي........................ 612
نمايش نمودارهاي مهم در مختصات قطبي...................... 613
ليماسيون................................................ 613
رُز چند برگ.............................................. 614
لمنيسكات (يا پروانه).................................... 614
مارپيچ ارشميدس.......................................... 614
مارپيچ لگاريتمي......................................... 614
نمايش خطوط و مقاطع مخروطي در مختصات قطبي................ 615
درسنامه2: محاسبهي طول قوس، مساحت محصور، سطح و حجم حاصل از دوران در منحنيهاي قطبي .......................................................... 617
طول قوس يك منحني قطبي................................... 617
محاسبهي مساحت محصور توسط يك منحني در مختصات قطبي........ 620
محاسبهي مساحت محصور بين دو منحني در مختصات قطبي......... 623
مساحت و حجم حاصل از دوران منحنيهاي قطبي................. 629
فصل هشتم: اعداد مختلط
درسنامه1: اعداد مختلط و خواص آن ............................... 633
اعداد مختلط............................................. 633
اعمال حسابي در اعداد مختلط.............................. 633
مزدوج يك عدد مختلط...................................... 634
خواص اعداد مختلط........................................ 634
ضرب داخلي و خارجي دو عدد مختلط.......................... 639
شكل قطبي اعداد مختلط.................................... 639
محاسبهي اندازه و آرگومانِ اعداد مختلط.................... 639
تبديل فرم دكارتي به فرم قطبي............................ 640
شكل نمايي عدد مختلط..................................... 641
ضرب و تقسيم اعداد مختلط به فرم قطبي يا نمايي............ 642
توان يك عدد مختلط و فرمول دموآور........................ 644
لگاريتم يك عدد مختلط.................................... 650
توابع مثلثاتي مختلط..................................... 652
توابع مثلثاتي معكوس..................................... 652
توابع هذلولي مختلط...................................... 653
درسنامه2: ريشههاي يك عدد مختلط و معادلههاي مختلط ................. 654
ريشهي يك عدد مختلط...................................... 654
چند نكته در مورد ريشههاي سوم عدد يك..................... 654
چند نکته در مورد ریشههای n ام عدد یک.................... 656
معادلات مختلط............................................ 658
چند قضيهي مهم........................................... 664
درسنامه3: نواحي در صفحه مختلط ................................ 666
بررسي معادلهي چند شكل خاص............................... 669
منابع و مراجع .......................................... 672
- دانلود فایل پاسخنامه آزمون های خودسنجی-چاپ اول و دوم
- دانلود فایل پاسخنامه آزمون های خودسنجی-چاپ سوم تا پنجم
- دانلود فایل پاسخنامه آزمون های خودسنجی-چاپ ششم تا نوزدهم
- دانلود فایل پاسخنامه آزمون های خودسنجی-چاپ بیستم
- دانلود فایل پاسخنامه آزمون های خودسنجی-چاپ بیست و یکم
- دانلود فایل پاسخنامه تشریحی آزمون های خودسنجی-چاپ بیست و دوم
- دانلود فایل قسمتی از کتاب ریاضی عمومی (1) - چاپ بیست و یکم
- دانلود فایل مثالهای اضافی برای تمرین بیشتر ـ ریاضی عمومی 1 -چاپ بیست سوم
- دانلود فایل قسمتی از کتاب ریاضی عمومی (1) - چاپ بیست و سوم
- نواب
با تشکر.
- مصطفی
- حسین
طبق فرمایش شما توابع براکتی در x هایی که داخل براکت را صحیح میکنند حد ندارد مگر اینکه طول مینیمم نسبی تابع داخل براکت باشد یا یک ضریب صفرشونده داشته باشد ، طبق این توضیحات چنین برمی آید که اگر نقطه ای که داخل براکت را صحیح میکند طول "ماکزیمم" نسبی تابع داخل براکت باشد حد نخواهد داشت ولی در مثال [4x-2x^2] میبینیم که ایکس مساوی یک، داخل براکت را صحیح میکند و طول "ماکزیمم" تابع هم هست ولی حد وجود دارد
ممنون میشوم این ابهام را رفع کنید.ممنون
- shahla
استادگرامی سوال ٨٨من باجمع بندی ص١٩٨حل میکنم ناپیوستگی ایجاد میشه زیرا٢<٢غلطه پس ناپیوسته
سوال ٨٩:استاد عزیز مگه نفرمودید هرجا ریشه ساده در قدر مطلق داشته باشیم مشتق ناپذیر،دراین سوال x=0ایا نباید نقطه مشتق ناپذیرباشد.
همچنین گفتیم تابع قدرمطلق درهمه نقاط مشتق پذیر به جز نقاط که تابع صفر اما مشتق صفرنیست
باتشکر از زحمتاتون
- شکیب
وقتتون بخیر
در فصل حد سوال ۲۲ صفحهی ۷۳،در تساوی دو تابع طبق نمودار دو تابع در سه نقطه همدیگه رو قطع میکنن پس طبق نکتهی گفته شده قبل سوال باید گفت که تابع در ۳نقطه حد داره ولی در کتاب جواب داده شده که در ۲ نقطه حد داره،میشه دلیلش رو توضیح بدید؟
- kiana
بله حق با شماست همان گزینه 2 جواب است.
- مریم دلور
- حمید
عرضی که داشتم اولا چرا پاسخنامه آزمون های خودسنجی 3 هر فصل رو چرا نذاشتید جسارتا؟!!
دوما توی آزمون دوم فصل مختصات قطبی سوال 9 ، توی فایل اشتباهی به جاش جواب یه سوال دیگه نوشته شده... میشه به ایمیلم جواب خود اون سوال رو بفرستین؟ ممنون میشم خیلی
- احمدرضا
اما اگر منظورتان ،آزمون شماره 1 است ،خیر نمی توان ساده کرد چون مخرج به لحاظ حدی برابر e^x است.موفق باشید
- حانیه
- مریم دلور
- مریم دلور
- حمید
ریاضی 1 چاپ جدید صفحه 788 تست 8
گزینه 4 اگر از r بتوان 2 فاکتور بگیریم مثل گزینه 1 میشه با یک توان بیشتر برای r
آیا گزینه 4 هم مانند گزینه 1 نمیتونه درست باشه؟
با تشکر و سپاس
- رضا کرمی میرعزیزی
- محمد
- محمد
خواهشمندم برای معرفی کتب استخدامی دبیری ریاضی خصوصا درس آموزش ریاضی از راهنمایی هایتان بهره مندمان سازید.چ کتابهایی مناسب است برای درس های آموزش ریاضی و خلاقیت ریاضی وبقیه دروس تخصصی؟
- مریم دلور
طبق کتاب ریاضی عمومی۱مدرسان شریف چاپ بیستم،ص۷۹۴،مثال ۴ ،درقسمت پایانی حل که انتگرال راتبدیل کرده چطوری uراانتخاب کرده جواب به صورت عبارتی برحسب tan وsec شده؟میدانیم که فرمول کسری یک بروی cos هم میتواند برحسب tanوهم sec بیایند اما درکل چگونه جواب اخر بدست امده است؟
- حمید
کتاب ریاضی 1 چاپ جدید من از صفحه ی 643 تا 658 را ندارد و در واقع به جای آن، صفحات 627 تا642 دو بار تکرار شده اند. اگر امکانش هست از صفحه 643 تا 658 را برام ایمیل کنید ممنون و متشکر میشم از لطفتون
- حمید
توی کتاب ریاضی یک چاپ جدید، صفحه 482 مثال 30
حاصل یک انتگرالی که میتونید توی آدرسی که گفتم ببینید، نوشتید برابره با منفی پی تقسیم بر 2
اونو میشه توضیح بدین؟ انتگرال سینوس آلفا ایکس تقسیم بر ایکس، از صفر تا بی نهایت، چجوری شده منفی پی تقسیم بر 2 ؟ ممنونم میشم اگه راهنمایی کنید مرسی
- ارش
در کتاب ریاضی 1 پایین صفحه ی 194 در قسمت (حالت اول) تصریح کرده اید که برای تعیین وجود یا عدم وجود مشتق در یک نقطه مانند X0 در توابع چند ضابطه ای باید حتما از تعریف مشتق استفاده کرد و نباید از قواعد مشتق گیری استفاده کنیم, پس چرا در صفحه 168 مثال 5 برای اینکه بفهمیم مشتق در نقطه ی 1 وجود دارد یا نه (مشتق چپ با راست یکسان هست یا نه ) از قواعد مشتق گیری بهره گرفته اید به جای تعریف مشتق ؟ آیا تفاوتی در این دو مسئله هست ؟
- ارش
1- در کتاب ریاضی 1 چاپ جدید صفحه 179 مثال 36 چه نیازی بود و به چه دلیل طرفین رابطه رو در X ضرب کردید ؟ آخه ضرب کردن در X حاصل نهایی مشتق رو عوض میکنه
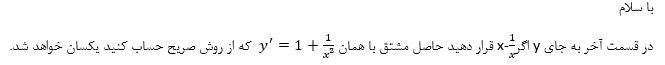
- محمد
در مثال 19 صفحه ی 132 کتاب ریاضی 1 ( فصل پیوستگی ) ، مجموعه نقاط ناپیوستگی تابع دو ضابطه ای را خواسته که حضرتعالی در پاسخ مثال اعداد زوج و فرد را جاگانه بررسی کرده اید و در مورد اعداد زوج به تابع ثابت y=0 و در اعداد فرد به تابع y=1 رسیده اید و در پایان نتیجه گرفته اید که تابع پیوسته می باشد ، سوال بنده اینست که وقتی برای هر گروه از اعداد به دو ضابطه رسیده اید بنابراین تابع نمی تواند پیوسته باشد چون در نمودار تابع پرش خواهیم داشت ، متشکر می شوم اگر رفع ابهام بفرمایید
- مرتضی
استاد در صورت امکان بفرمائید دسترسی به پاسخنامه آزمون سطح A از چه راهی امکانپذیر میباشد . متشکر
- javad
ببخشید میخواستم بدونم که تمام تست هایی که توکتاب ریاضی عمومی آوردید تست های کنکور هستند یا سواالات تالیفی هم هستن؟
ممنون میشم پاسخ بدید
- کیوان
- مرضیه علایی
- محبوبه
تابع x*2/3 + y*2/3 =1 در نقاط یک و منفی یک تغییر تقعر میده اما ایا در این نقاط مشتق هم داره که عطف محسوب بشه؟ یا اینکه این تابع کلا فاقد عطفه؟
- شقایق پوروثوقی
پاسخ تشریحی آزمون های خودسنجی را در سایت قرار می دهید؟
- مهدی
- milan
بنده مشکلم اینه ک چرا دلتا ایکس یک اومده بعبارتی این یک از کجا بدست میاد؟ممنون میشم
- مجید
- فرانک
پاسخنامه تشریحی آزمونهای خودسنجی ریاضی1 چاپ بیستم رو سایت نیست
- مهران
تو صفحه 268 کتاب ریاضی 1 چاپ 20، نقطه عطف رو تعریف میکنید به صورت نقطه ای که میشه خطی به نمودار مماس کرد و مشتق دوم هم در دوطرف این نقطه عوض بشه...
حالا سوال من اینه که در منحنی: Y^2+(X-1)^2=1
یعنی دایره ای که به محور Yمماس شده، نقطه 0 نقطه عطف حساب میشه؟
چون هم مماس به نمودار میشه کشید تو اون نقطه، هم نقطه عطف بالا و پایین محور X یعنی دو طرف نقطه (0,0) عوض میشه. و تو تعریف هم نگفتید منحنی حتما باید تابع باشه...
این که این نقطه نقطه عطف هست یا نه تو جواب مثال 50 صفحه 270 تاثیر مستقیم داره.
ممنون.
در مبدا مشتق وجود ندارد اما اگر برای y<0 و y>0 که در دوطرف این نقطه قرار دارند به مقدار مشتق توجه کنیم از یک طرف ∞ و از طرف دیگر -∞ به دست می آید.پس طبق توضیحات پاراگراف زیر صفحه 268 این نقطه ،عطف محسوب نمی شود.می توان این دایره را به صورت پرامتری x=1 cost و y=sint هم نوشت و متوجه شد که در t=Π یعنی همان نقطه ی مبدا ،عطف وجود ندارد.مثل توضیحات مثال 50 صفحه 270.موفق باشید
- ایمان حسین زاده
- علیرضا
با تشکر از پاسخگویی بی دریغ شما به سوالات
در مورد تست 23 صفحه 285 چاپ بیستم ریاضی یک
من بسط مکلورن تابع را نوشتم که شد {3x-(1/3x)} و بعد از آن مشتق گرفتم که شد {3+(1/3x^2)} و از آنجا نتیجه گرفتم که مشتق تابع f در حوالی صفر همواره مثبت است پس در یک همسایگی f صعودی است.
آیا استدلال من ایراد دارد؟
با سپاس فراوان
- علیرضا
در صفحه ی 241 چاپ بیستم ریاضی عمومی یک چرا زاویه ی بین دو نیم مماس برابر (pi-alpha) می شود؟
من احساس می کنم همان alpha می شود و در یک منبع هم دیدم که زاویه ی بین دو نیم مماس را هم مثل زاویه ی بین دو منحنی حساب کرده(یعنی همان alpha)
خیلی ممنون می شوم اگر راهنمایی بفرمایید
با تشکر
- علیرضا
در صفحه ی 197 چاپ بیستم ریاضی یک با مشکل مواجه شده ام و آن این که در پایین صفحه(سطر پنجم از پایین) آنجایی که تعریف(x)'h به ازای a=b+1 را نوشته اید احساس می کنم در جمله ی دوم ضریب a اضافه است و اشتباه نوشته شده
آیا درست فکر می کنم؟
ممنون میشوم اگر راهنمایی بفرمایید.
با تشکر
- نادر
- Sajjad
خسته نباشين
استاد من توو رياضي ١ چاپ بيستم صفحه ٤٥٨ مثال ٣١ طرز تبديل انتگرال به Lim رو نفهميدم...يعني توو هيچكدومشون نفهميدم مقدار p كه توان x ميشه چجورى مياد..اگه لطف كنين يه توضيح مختصر بدين ممنون ميشم
و اينكه استاد من رياضي ١ رو تا هفته اول مهر تموم كنم رياضي ٢ رو ميتونم تا آزمون ها به يه جايي برسونم؟ يا بايد تا آخر شهريور تموم شه رياضي ١؟رشتمم MBA هستش
عذر ميخوام يكم طولاني شد..مرسي
- علی صلواتی زاده
سوال 10 آزمون سطح A فصل 1 (تابع) چگونه حل میشه؟
- mojtaba
- mojtaba
- محسن
منظورم از منفی شدن ایکس با منفی شدن وای در مثال ۳۹ صفحه ی ۱۱ چاپ ۲۰، این بود که چه طور از رابطه ی: a^y=(x+((x^2)+1)^0.5)
به رابطه ی: a^(-y)=-x+((x^2)+1)^0.5
رسیدید؟
- محسن
در صفحه ی ۱۱- مثال ۳۹، چرا با منفی کردن "وای"، "ایکس" نیز منفی شد ؟
- عليرضا سهرابي زاده
صفحه ٦٥٥ رياضي ١، مثال ١١، اگه تو صورت n رو ببريم پشت ln ، تو مخرج هم n و n+1 رو ببريم پشت ln ، ميتونيم n*n+1 رو از صورت و مخرج حذف كنيم و اگه حل كنيم جوابش ميشه گزينه ٢، با اين كه راه حل شما هم درسته، ولي دوتا جواب مختلف داره به دست مياد
ميخواستم بدونم مشكلي داره آيا راه حل من؟
پيشاپيش ممنون
- ادمین
اول از کتابهای بسیار خوبه ریاضی ازتون تشکر می کنم بعد اینکه در مدت باقی مونده مدت زمان مطالعه باید در طول روز چقدر باشه و بیشتر چه درسی رو بخونم ؟من یه دور کامل ریاضی عمومی 1 و2 را خوندم
با تشکر
- فربد
استاد صفحه 545 زیاضی 1، مثال 7، گفته شده مساحت محصور به یک حلقه، من الان متوجه نشدم چرا جواب در 2 ضرب شد!!؟ از کجا باید فهمید که یک حلقه شکل هم در ربع اول و هم در ربع دوم قرار داره؟؟ یعنی یک حلقش در ربع اول و یک حلقش در ربع دوم نیست به صورت متقارن؟
سوال دیگه ای که داشتم بعضی کتابا علامت قدرمطلق رو دور خود تابع گذاشتن ولی شما دور کل انتگرال، فرقی داره یا یکیه؟؟
اگر حدود انتگرال را درست نوشته باشید ایرادی ندارد که قدر مطلق بیرون باشد.وقتی قدر مطلق را داخل قرار دهیم باز هم بایدبا توجه به حدود انتگرال تعیین علامت کنیم،در هر صورت اگر در تشخیص حدود اشتباه نکنید این دو روش یکسان هستند.
- بانی امین نژاد
- سالار نوذري
- فربد
صفحه 789( تست های طبقه بندی شده درسنامه 1) سوال 15 رو با یه روش و سوال 20 رو با یه روش دیگه حل کردین، چرا سوال 20 رو نمیشه با روش سوال 15 حل کرد؟؟ تفاوت این دو سوال در چیه؟
یه سوال دیگه که داشتم، تست های طبقه بندیشده، برخی از رشته ها رو شامل میشه یا تمام رشته هایی که در اون سال از اون مبحث سوال داشتن؟؟
- فربد
چرا از coshy=2 نتیجه میگیریم بی نهایت جواب مختلط داره؟؟ خب ما وقتی
پی x=k رو به رو جلوی کمان cos قرار میدیم حاصل یا مثبت 1 میشه یا منفی 1 و به ازای این دو تا معادله رو حل کردیم و به جواب coshy=2 رسیدیم، که y میشه برابر معکوس کسینوس هیپربولیک 2، ما به ازای هر k که یک مقدار برای x به دست می اید جلوی cos یا یک مثبت میشه یا منفی یک، و ما هم معادله رو حل کردیم، من متوجه نمیشم چرا باید بی نهایت جواب بشه؟؟؟
- فربد
برای sin و cos دو تعربف جداگانه( تعریف و نکته 10) نوشته شده، کی باید از نکته و کی از تعریف استفاده کنیم؟؟ چجوری تشخیص بدیم کدوم بهتره؟
- فربد
در کسر دوم راه حل، در مخرج کسر به علامت منفی بین e ها نباید مثبت باشه؟
- فربد
در پایین صفحه نوشته شده، تقارن منحنی نسبت به ناحیه اول و چهارم، تقارن نسبت به ربع اول و سوم نیست؟؟؟
- فربد
در روش اول یا روش دوم، قسمتی که گقته شده در این بازه کسینوس(پیr) منفی هستش، منظور کدوم بازه هستش؟ چجوری بازه رو پیدا میکنیم که به این نتیجه برسیم؟
- فربد
میشه بازه را 0 تا 2پی سوم در نظر گرفت و جواب اخر رو در 2 ضرب کرد؟؟مثل مثال 10 که بازه را 0 تا 2پی سوم در نظر گرفتیم؟؟
- فربد
در اخر سوال برای تانژانت(3 تتا) برابر 1، دو زاویه به دست امده( پی دوازدهم و 5پی دوازدهم) ، چرا زاویه 9پی دوازدهم به حساب نمیاد؟؟
9پی دوازدهم یا همون 135 درجه هم در دوره تناوب تانژانت( بین 0 تا پی قرار داره)
در وسط راه حلم هم به به جای سینوس 3(تتا به علاوهn پی)، نوشته شده منفی 1 به توان 3n، ایا فرقی داره به جای 3n، منفی 1 به توان n نوشته بشه؟؟( دلیل خاضی بوده که 3n نوشته شده؟؟)
- فربد
صفحه 782، مثال 1، وقتی که وقتی زاوبه بین پی چهارم و پی دوم، که مقدار r منفی میشه، به جای ربع اول، ربع سوم شکل رسم شده، از کجا باید تشخیص بدیم که در ربع سوم به جای ربع اول باید شکل رسم بشه؟؟
- سالار نوذري
- سهراب
در فرمول لایب نیتز صفحه 131 ریاضی1 پرانتز بزرگ به چه معنی هست؟ (به زبان ریاضی یعنی چی ؟) و روش حل اون پرانتز در حل خود فرمول لایب نیتز چجوری هستش؟
پرانتز به معنی ترکیب است-انتخاب r شی ازn شی .قسمت یادآوری کتاب را مطالعه کنید.موفق باشید















